集合论为人类认识无穷提供了公理化的理论基础,从集合论出发,我们可以得到很多有意思的结论。
比如,人类运用各种符号系统可以计算求解的问题,一定小于问题的总和。
自计算机问世以来,人类技术进入加速发展的快车道,计算机理论和硬件的革新带来的是人类计算处理复杂问题能力的爆炸式增长。假如真如库兹维尔所说,人类技术是以指数的形式增长,那科学和技术发展的尽头是什么?会是所谓的“技术奇点”吗?人类的认识和计算存在极限吗?
如果以上说法只是基于人们的经验和猜想,那有没有可能从纯粹的逻辑上证明计算的极限存在与否?
集合论可以证明,不可计算的问题一定存在。
证明之前,对“可计算的问题”做一个明确的定义:如果一个问题可计算,则这个问题可用函数(function)表示并且可以用计算机程序算出函数的值。
下面要证明这个命题,需确认两点:
- 一切计算机程序,不管用何种语言编写,都是可列的。
- 一个无穷可列集映射到它自身的函数有无穷个,且不可列。
第一点很容易理解,不管是何种计算机语言写成的程序,都可以看作是有限的字母表组合成的一串字符,且字符的个数一定是有限个(程序首先要能被写出来)。这和从有限整数集合{ 0,1,2,3,4,5,6,7,8,9 }挑选数字组成一个个自然数一样,这些自然数组成的自然数集是可列的,同理,计算机程序组成的集合也是可列的。
要证明第二点,同样可以借助自然数集来说明。自然数集是一个可列集,考虑将自然数集映射到它自身的函数$f$,假设
用$d_{1},d_{2},d_{3},…d_{n}…$组成一个$[0,1]$之间的无限小数
这样,每个小数就对应一个不同的$f$。我们已经证明,实数集是不可列集,所以$f$组成的集合同样也是不可列集。同理可做推广,任一无穷可列集映射到它自身的函数都构成了一个不可列集。
两个条件都已具备。第一,组成可计算问题的函数集是可列集;第二,证明了还存在不可列的函数集合,因此也就从理论上证明了不可计算问题的存在。
尽管借助集合论这样一个公理化的数学理论可以证明不可计算问题的存在,但最早帮助人们认识计算的极限的,却是一台小小的机器——图灵机。
图灵机非常简单,可以把它看作一台最简单的计算机。现在电脑能做的计算,只要给予充分的时间和耐心,图灵机同样能够在有限步骤内实现。可以说,图灵机是所有现代计算机的亚当夏娃,那么,图灵当初为什么要造这样一台机器出来呢?
时间回到1935年,阿兰·图灵刚刚结束他在剑桥国王学院4年的本科学习,进入了研究生院继续追寻他对数学的兴趣。此时,距离大数学家希尔伯特1900年世纪之初提出著名的23个问题,过去了35年。19世纪后期,数学界兴起了一场公理化运动,为的是去除基于直觉或经验的朴素概念所带来的模糊,进一步推动数学走向抽象、形式化,以求达到绝对的严密。到1900年巴黎的数学大会上,希尔伯特宣布:“借助集合论可以建造整个数学大厦……今天我们可以宣称绝对的严密化已经实现了!”但是,他不得不承认,在即将建成的这座大厦里,仍有一些让人不安的疑惑。其中就包括23问中的第二个问题:算术系统的相容性。算术系统的相容性问题后来又引申为三个基本问题:
- 数学系统是否完备。是否所有命题都可以被证明或证伪?
- 数学系统是否一致。算术系统会否推出相互矛盾的命题?
- 数学系统是否可判定。能否通过机械化的计算,判定命题的对错?
当一个数学系统同时具备完备性、一致性、可判定性时,之上建立起的数学大厦才是安全的。
不幸的是,1931年,一个叫哥德尔的年轻人提出并证明了两条定理:
- 任何包含皮亚诺算术公理的数学系统,只要满足一致性,就必然存在不能被证明或证伪的命题。
- 任何包含皮亚诺算术公理的数学系统,如果它是一致的,那么不能从体系内部证明该系统的一致性。
这就是著名的“哥德尔不完备性定理”,它击碎了希尔伯特雄心勃勃的设想,证明了根本不可能实现算术系统完备性和一致性的相容。这也就相当于告诉人们,在真理和证明之间,还存在着一条不可逾越的鸿沟,数学建立起的逻辑大厦并不能装下所有的真理。数学凭借自己的逻辑的力量,证明了数学的力量是有界限的。
尽管“哥德尔不完备性定理”已经宣告算术系统相容性的失败,但它还留下了一个问题:数学系统可判定性与其它两个问题的关系。完备的数学系统是可判定的吗?
想要解决这个问题,首先要搞清楚什么是“机械计算”。在当时,或许有人可以大致说出“机械计算”的含义,但没有人知道它到底如何实现,这是计算机诞生的史前时代——直到图灵机诞生。
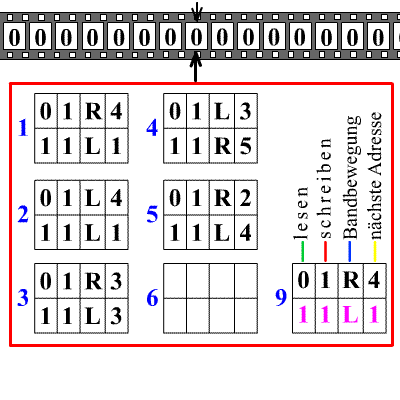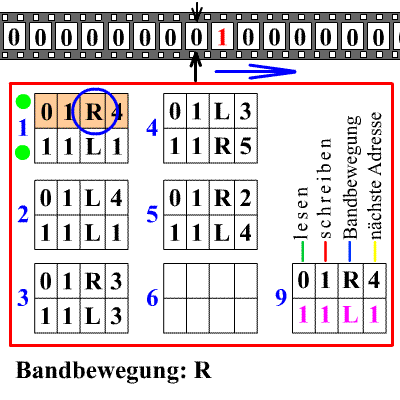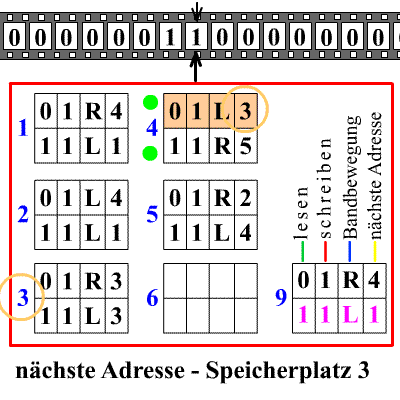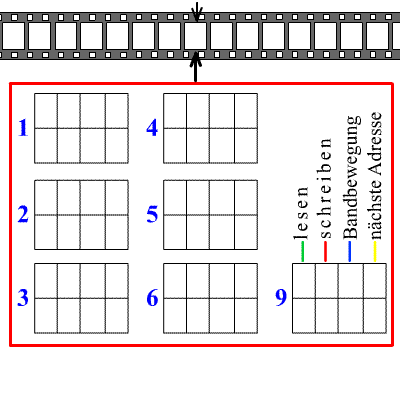
图灵说,机器能进行的计算就是“机械运算”,但他创造的图灵机绝对不止这么简单。图灵机强大的地方在于:存在一种通用图灵机,它可以模拟任何一台图灵机。这也就是说,通用图灵机可以成为任意一台图灵机执行它的计算过程,是所有机器的机器。那么,依靠图灵机,所有可计算问题均能被解决。那自然而然的,我们就要问,图灵机这么强大,存不存在图灵机无法计算的问题?换句话说,会不会有问题是图灵机永远也无法算出来的?这就是著名的图灵机“停机问题”。
图灵机什么时候会停机?存不存在一个图灵机,可以判断图灵机是否会停机?假如存在,我们可以把数学中许多悬而未决的猜想,如哥德巴赫猜想、黎曼猜想等,扔给图灵机去计算,然后用这台特殊的图灵机判断执行计算的图灵机是否会停机,如此一来这些困难的数学猜想就都能通过停机问题解决。
可惜的是,这样一台能解决停机问题的图灵机并不存在。
图灵机是一个如此强大的系统,强大到存在图灵机可以模拟任意一台图灵机,但这埋藏着它的致命弱点:可模拟的对象包括它自身。
危险的自我指涉,悖论往往由此产生。罗素悖论、哥德尔不完备定理、说谎者悖论……本质都是矛盾的自我指涉。
假设存在一台可以判断图灵机停机问题的图灵机 P。
现有一台图灵机R,为其输入的编码为< M >,R需要调用图灵机P,判断图灵机M在输入编码< M >上会不会停机。假如M会停机,R将进入死循环;假如M不会停机,R将会停机。
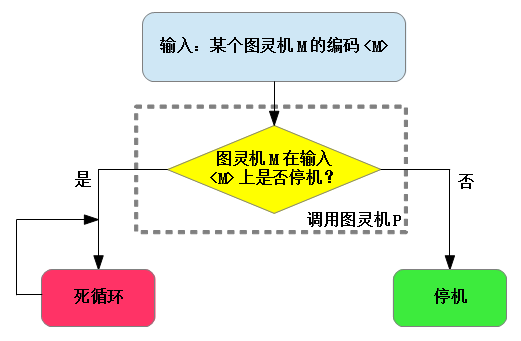
若令图灵机M为R自身,输入编码< R >,令R执行计算。假如P判断R在< R >上会停机,则R进入死循环,R不会停机;假如P判断R在< R >上不会停机,R将停机。这样就产生了悖论,说明这样一个图灵机P根本不存在。
如此一来,就证明了存在图灵机不能在有限时间内求解的问题。1936年,图灵将发现写成论文《论可计算数,及其在可判定性问题上的应用》(On Computable Numbers, With an Application to the Entscheidungsproblem),证明了希尔伯特第三个问题可判定性也不可能与完备性相容,希尔伯特关于算术系统相容性的期望完全落空。
哥德尔不完备性定理告诉我们,即使是一个严密公理化的数学系统,仍然可能存在不可证明的命题;
图灵机“停机问题”则说明,即使所有命题可被证明或证伪,人类也无法依靠机械计算对所有命题做出判断。
信息论观点
柏拉图主义:认为世界有确定的知识,这种知识是变化的事实背后永恒不变的本质,人要做的是追求、认识这些知识。
“The only true being is founded upon the forms, the eternal, unchangeable, perfect types, of which particular objects of sense are imperfect copies。”
数学柏拉图主义:数学发现的是独立于思考的人、思想、事物的确定性知识。数学家做的是发现而不是发明。
Mathematical objects are independent of intelligent agents and their language, thought, and practices.
信息论认为,所有信息中,有用的信息只占极少数(测度为0),虽然数学公理系统可能是不完备的,但数学是对有用知识的逼近。
参考