0%

命题逻辑

发表于 更新于 分类于 阅读次数： Valine：

语法和语义是符号逻辑的基本要素。

语法中推出的结论，可以在语义中找到一致的对应，称该符号逻辑系统是“可靠（soundness）”的；

语义中的结论，都可以从语法中推出来，称该符号逻辑系统是“完备（completeness）”的。

验证程序的可靠性（程序是正确的）有两种方法：

  1. 霍尔逻辑：使用公理描述程序语句对于计算状态的改变，一步步验证程序语句的逻辑正确。
  2. 软件测试：验证输入输出是否满足程序规约要求。


命题逻辑的语法

字母表

字母表的组成：

  1. 命题符：$P_0,P_1,P_2,…P_n,n\in \mathbb{N}$，记命题符集$PS=\{P_n|n\in\mathbb{N}\}$
  2. 联结词：$\neg,\wedge,\vee,\to$
  3. 辅助符：( , )

命题

  1. 命题符为命题；(原子句式)
  2. 若A，B为命题，则$(\neg A),(A\wedge B),(A\vee B) ,(A\to B)$也为命题；（复合句式）
  3. 命题仅限于此。

Bacus-Naur Form命题定义：$\psi::=P|(\neg\psi)|(\psi_1\wedge \psi_2)|(\psi_1\vee\psi_2)|(\psi_1\to \psi_2)$, 其中$P\in PS$。这种建构句式的方式成为递归定义（recursive definition）。

命题集

所有命题的集合PROP是满足以下条件最小集合：

  1. $PS\subseteq PROP$
  2. 若$A\in PROP$，则$\neg (A)\in PROP$
  3. 若$A，B\in PROP$，则$ (A\wedge B),(A\vee B),(A\to B)\in PROP$

构造序列

一个有穷序列$A_0,A_1,A_2,…A_n$，若对任意$i\le n$都满足下列条件之一：

  1. $A_i\in PS$
  2. $\exists k<i$,使$A_i$为$(\neg A_k)$
  3. $\exists k,l<i$,使$A_i$为$(A_k\wedge A_l)或(A_k\vee A_l)或(A_k\to A_l)$

记$A$为$A_n$，则序列$A_0,A_1,A_2,…A_n$称为A的构造序列。


命题逻辑的语义

对于所有命题的集合，只要给定最基本的命题符集PS中的命题以真假，则所有命题皆可推出真假。这样一来，原本只是一些无意义的符号的命题就被赋予了语义。这个过程可表示为：

​ 对于任意的赋值$\nu:PS\to\{T,F\}$，有解释$\hat\nu:PROP\to\{T,F\}$

从赋值了的原子命题向复合命题推广语义判断的桥梁，是联结词和真值表：

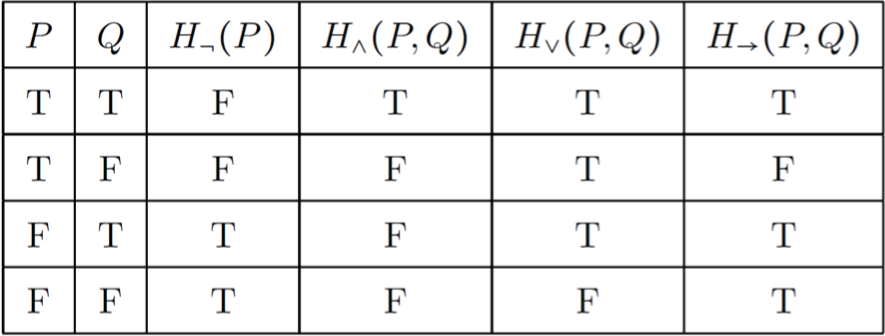
image-20200225001445007

其中 $H_{\neg}:B\to B$为一元布尔函数，$H_{\flat}:B^2\to B$为二元布尔函数（$_{\flat}$为$\wedge,\vee ,\to$），$H_A:B^n\to B$为n元布尔函数，又称真值函数。可以理解为，联结词是由真值表定义的，每个联结词对应真值表的一个二元布尔函数。


将上述产生语义的过程用规范语言表达，可以给出命题语义的归纳定义：

  • 赋值：$\nu$为赋值，指给命题符一个真伪的判断：$PS\to\{T,F\}$，也即对于命题符$P_i$，使$\nu(P_i)=T\ or\ F$
  • 解释：$\hat \nu $为解释，指对任意命题的真伪判断：$PROP\to\{T,F\}$，详细的判断规则如下：
    1. $\hat \nu(P_i)=\nu(P_i)$，对命题符而言，它的解释就是赋予它的布尔值
    2. $\hat \nu(\neg P_i)=H\neg(\hat v(P_i))$
    3. $\hat \nu({P_i}_{\flat}P_j)=H_{\flat}(\hat \nu(Pi,P_j))$，其中$_{\flat}$为$\wedge,\vee,\to$


可以证明，对于一个命题A，要判断其真伪，唯一有关系的是最底层的命题符的真伪；只要基本命题符的赋值一致，就不会推出相悖的结论。这些最底层的命题符也叫做自由变元（FV）。


现在我们赋予了所有命题以语义（真假值），对于一些特定的复合命题及其真假值，可以定义一些命题的关系：

  1. 蕴含关系（implication）

    记为$\phi_1,\phi_2,…\phi_n \vDash \psi$。它表示的是当$（\phi_1 \wedge\phi_2…\wedge \phi_n) \to \psi$为恒真句时$\phi_1,\phi_2,…\phi_n$和$\psi$的关系。

  2. 等值关系（equivalence）

    记为$\vDash \phi \leftrightarrow\psi$。它表示的是当为$\phi \leftrightarrow\psi$恒真句时$\phi$和$\psi$的关系。

  3. 不一致（inconsistency）

    记为$\Gamma\vDash$。它表示的是当为$\Gamma$中所有命题的连言$\wedge$为矛盾句时它们的关系。从一个不一致的前提可以推出任何结论，从一个说谎的人嘴里什么都可以得到。

  4. 一致（consistency）

    记为$\Gamma \not \vDash$。它表示的是当为$\Gamma$中所有命题的连言$\wedge$不是矛盾句时它们的关系。


有效论证：当前提和结论具有蕴含关系时，称论证是有效的。

PS. 描述赋值、联结等动作使用的这一套固定的语言，称为元语言（meta-language）。如$v\vDash_{\neg}P\to Q$

PPS. 归谬法的原理：

要证$P \vDash Q$是一个有效论证

即证$P \to Q$为恒真句

只要假设结论为False，证$\neg Q\wedge P$为False（得到矛盾）即可，因为：

$\neg(\neg Q\wedge P)$为True，$\vDash \neg(\neg Q\wedge P) \leftrightarrow (Q \vee \neg P) \leftrightarrow (P\to Q) $


析合范式和合析范式

现在我们知道，给定一个命题，可以由真值函数$H_A:B^n\to B$推断命题的真伪；那么反之，如果给定的是一个真值函数f，是不是也能找到一个命题A使得$f=H_A$呢？

析合范式DNF$(\vee \wedge-nf)$：对若干命题先合取再析取：$ \stackrel{i}\vee (\stackrel{k}\wedge P_{i,k)}$

合析范式CNF$(\wedge \vee -nf)$：对若干命题先析取再合取：$ \stackrel{j}\wedge (\stackrel{k}\vee P_{j,k)}$

可以证明，给定真值函数$f:B^n\to B$，存在为$\vee \wedge-nf$的命题A，使$f=H_A$；也存在为$\wedge \vee -nf$的命题A’，使$f=H_{A’}$。

析合范式

图1

图2

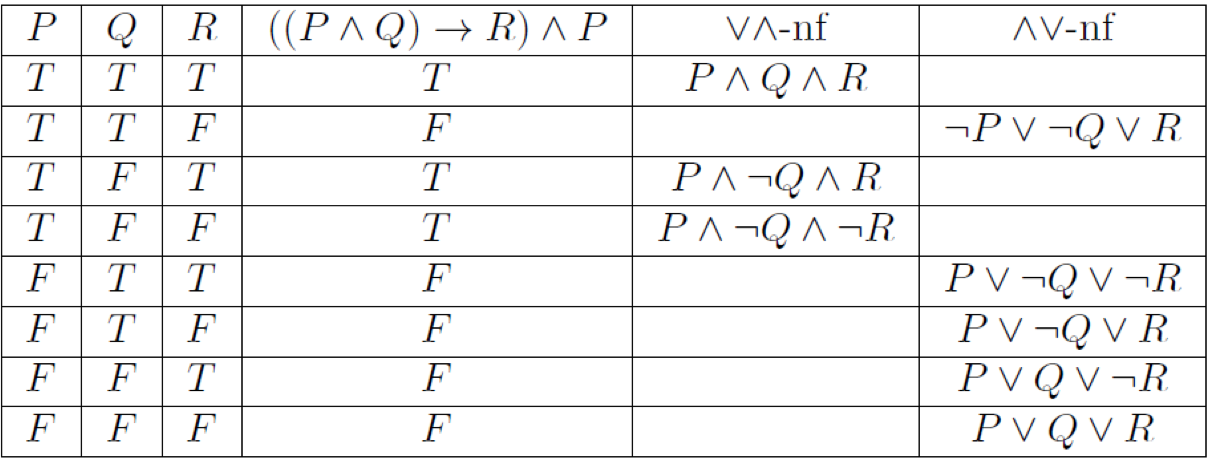
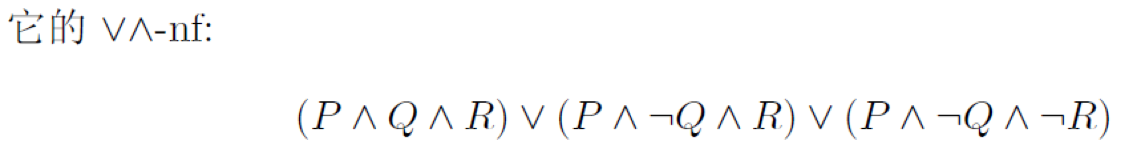
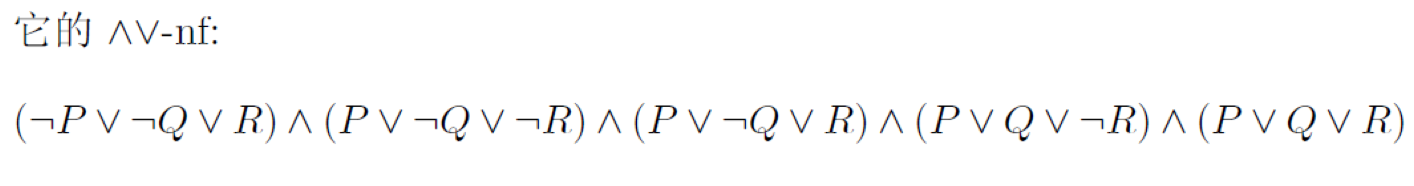
对于一个由命题P定义的真值函数f，以及f的析合范式命题A、合析范式命题A’，称P、A、A’是逻辑等价的，记为$P\simeq A \simeq A’$。逻辑等价的命题其真值函数相等。另外也可以证明，与P逻辑等价的$(\vee \wedge-nf)$$、(\wedge \vee -nf)$形式的命题B、B’就是f的析合范式A和合析范式A’。

任意给一个真值函数$f$，因为仅用$\neg ,\wedge, \vee $三个符号就可以构造一个命题A使得$H_A = f$，所以$\{\neg,\wedge,\vee\}$被称为具有函数完备性（functional complete）的联结词集。另外，$\{\neg,\to\},\{\neg,\wedge\},\{\neg,\vee\}$这些也都具有函数完备性。


真值树系统

从古典逻辑的发展历史来看，有三种经常被提到的语法演算系统：

  1. 公理系统（Axiom System）
  2. 自然演绎系统（Natural Deduction System）
  3. 真值树系统（Tableaux System）

我们这里关心的是如何做证明，研究的是语法的蕴含关系，与之前的语义蕴含关系不同，蕴含符号不是$\models$而是$\vdash$。

逻辑刚刚建立时，古希腊人认为推理的基础是一些简单直白到人人都会认同的公理（Axiom），依据这些公理及其包含的推理规则，推导出新的理论，称为定理（Theory）。这是公理系统的方法。

但公理系统的推导与证明有些过于艰难。使用公理系统工作的人手里拿着的是一把锤子，拿最简单的工具当然可以建造宏大的宫殿，但需要极大的耐心、一些天赋、以及世世代代的努力。对于现代人来说，锤子显得有些原始，他需要的是更轻松省力的工具。在1935年，Gentzen第一次提出了自然演绎法。自然演绎法舍弃了公理，仅保留推理规则，事实上，引入了更多的推理规则。可以用的规则越多，证明就变得越简单。

而真值树系统就像加减法的竖式计算，学会使用它可以不依靠任何天赋和洞见就能完成证明。要证明的一些命题在树顶，要做的是从树顶向下分解，直到分成一个个命题符（原子句式），它们就是树的“根”。

下面看看如何种下你的第一棵“真值树”：

  1. 把你想证明的命题公式放到树顶

  2. 按照这些规则向下发展树根：

  3. 把出现矛盾的分支关闭：

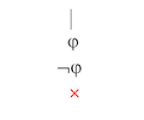
  4. 若最后全部分支都封闭，则原命题为假，是矛盾句；若存在开放的分支，试着把原命题取反，再走一遍真值树，如果全部分支封闭，则原命题是恒真句；如果仍然存在开放的分支，则原命题是偶真句。对于第一种情况，称组成原命题的句式是不相容的；对后两种情况，称组成原命题的句式是相容的。学过线性代数的人会发现，线性方程组的有解、无解就对应着这个由方程组成的连言式相容或不相容的概念，事实上，也确实是这么叫的：相容的方程组至少有一个解，否则就称这个方程组是不相容的。

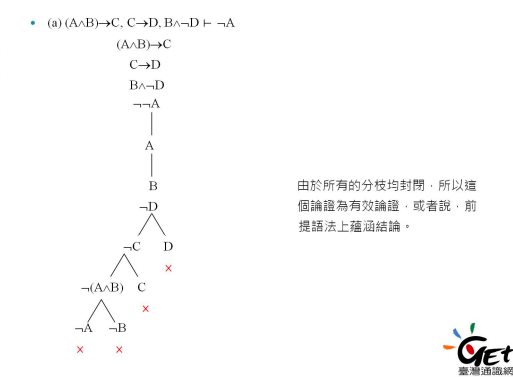
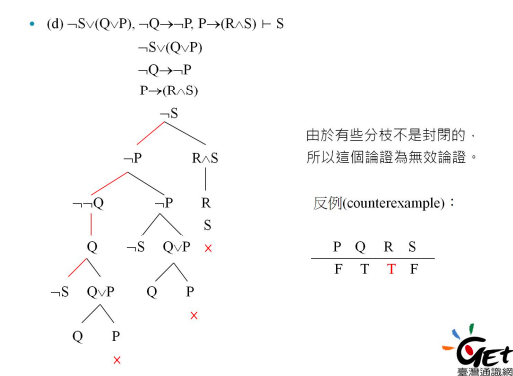
    对于蕴含证明来说，将结论取反与前提放在一起组成连言式作为树顶，若全部分支封闭，则论证为有效论证；反之为无效论证。（归谬法）

​

图片来自台湾通识网 傅皓政老师《逻辑》课讲义


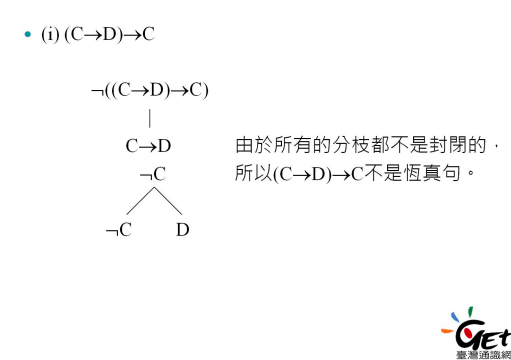
命题逻辑的自然推理系统





参考

台大开放式课程 傅皓政《逻辑》