PCA、CCA、PLS

Principal Component Analysis（主成分分析）、Canonical Correspondence Analysis（典型相关分析）、Partial Least Square（偏最小二乘）

从多元线性回归说起

•目的：p个自变量x 对1个因变量y的回归

$Y=y,\ \ \ \ \ \ X=\left[ \begin{matrix} x_1\ x_2\ \cdots\ x_p \end{matrix} \right] ,\ \ \ \ \ \ \beta=\left[ \begin{matrix} \beta_1\\ \beta_2\\ \vdots\\ \beta_p \end{matrix} \right]$

•回归方程为：

$Y=X\beta+\epsilon$

•手上有n个观测（相当于训练集），用这n个观测来估计β

$Y=\left[ \begin{matrix} y_1\\ y_2\\ \vdots\\ y_n\\ \end{matrix} \right],\ \ \ \ \ \ X=\left[ \begin{matrix} x_{11}& x_{12}& \cdots& x_{1p}\\ x_{21}& x_{22}& \cdots& x_{2p}\\ \vdots &\vdots& \ddots & \vdots\\ x_{n1}& x_{n2}& \cdots& x_{np}\\ \end{matrix} \right] ,\ \ \ \ \ \ \beta=\left[ \begin{matrix} \beta_1\\ \beta_2\\ \vdots\\ \beta_p \end{matrix} \right]$

根据最小二乘法：

$\beta=(X^TX)^{-1}X^TY$ 一个小问题：若Y也有多个变量时怎么办？

假如Y有q个变量，给Y添加一个长度为q的维度就可以了，回归公式仍然成立。

•但多元线性回归存在缺陷：

1.理论假设需要满足自变量x1, x2 ··· xp互相独立（现实中往往具有多重共线性）；

2.当X的变量数非常多时，求解β时需要求$(X^TX)^{-1}$，这是一个p*p的高维方阵，求解困难；

3.而且不一定每个x因子都是显著的，包含冗余信息。

PCA（主成分分析）

•目的：提取变量中最能代表其特征的成分

•变量X（已标准化）

$X=\left[ \begin{matrix} x_1\ x_2\ \cdots\ x_p \end{matrix} \right]$

有n个观测时X就是n*p的矩阵

•记u是X的一个主成分，a为载荷向量

$u=X\textbf{a},\ \ \ \ 其中\ \textbf{a}=\left[ \begin{matrix} a_1\\ a_2\\ \vdots\\ a_p \end{matrix} \right]$

•要求是a使得u的方差最大（其实就是最小二乘），即令

$Var(u)=\frac{\textbf{a}^TX^TX\textbf{a}}{n-1}=\textbf{a}^TC_{xx}\textbf{a}$

最大

「为什么要令u的方差最大呢？」下面以简单的X有两个变量的例子说明：

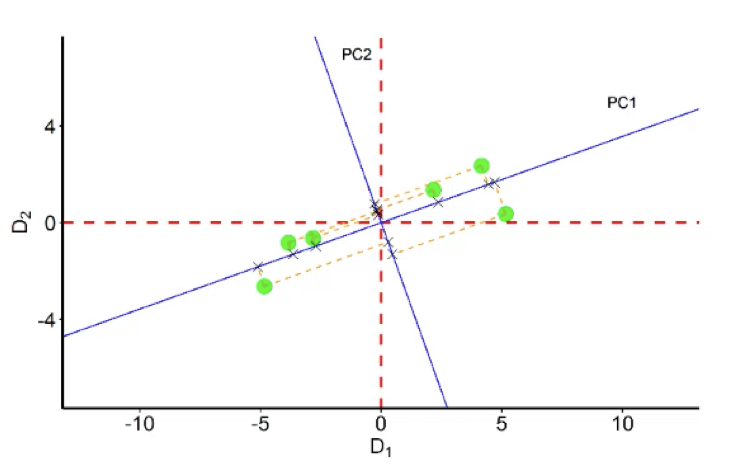
Var(u)的几何意义其实是X在主成分载荷向量a上投影点到原点距离平方和，可以从两个角度来理解这个问题。

令Var(u)尽量大，也就是该主成分载荷向量（PC1蓝线）可以把X的样本点分得尽量开，更能反映样本的差异（差异其实就是特征）；另外，这其实也是最小二乘思想，令Var(u)最大，就是令各样本点到PC1的距离平方和最小（想想看，各样本点到原点的距离是固定的）。

•求主成分的问题就可以提炼为

$maximize (\textbf{a}^TC_{xx}\textbf{a})\\ 约束条件：\textbf{a}^T\textbf{a}=1$

最终转化为熟悉的求特征值和特征向量问题，保留k个主成分原来p维的X就降维到了k维。

CCA（典型相关分析）

•目的：提取出因变量和自变量中最相关的成分

•因变量Y和自变量X（都已标准化）

$Y=\left[ \begin{matrix} y_1\ y_2\ \cdots\ y_q \end{matrix} \right],\ \ \ \ \ \ X=\left[ \begin{matrix} x_1\ x_2\ \cdots\ x_p \end{matrix} \right]$

•记典型变量u，v，分别是X各变量和Y各变量的线性组合

$u=X\textbf{a},\ \ \ \ \ v =Y\textbf{b}, \ \ \ \ \ 其中\ \textbf{a}=\left[ \begin{matrix} a_1\\ a_2\\ \vdots\\ a_p \end{matrix} \right] ,\ \ \ \ \ \textbf{b}=\left[ \begin{matrix} b_1\\ b_2\\ \vdots\\ b_q \end{matrix} \right]$

•要使得u，v相关性最大，即令相关系数

$Corr(u,v)=\frac{COV(u,v)}{s_us_v}=\frac{\textbf{a}^TX^TY\textbf{b}}{\sqrt{\textbf{a}^TX^TX\textbf{a}}\sqrt{\textbf{b}^TY^TY\textbf{b}}}=\frac{\textbf{a}^TC_{xy}\textbf{b}}{\sqrt{\textbf{a}^TC_{xx}\textbf{a}}\sqrt{\textbf{b}^TC_{yy}\textbf{b}}}$

最大

•求典型相关变量的问题就提炼为

$maximize(\frac{\textbf{a}^TC_{xy}\textbf{b}}{\sqrt{\textbf{a}^TC_{xx}\textbf{a}}\sqrt{\textbf{b}^TC_{yy}\textbf{b}}})\\ 约束条件：\sqrt{\textbf{a}^TC_{xx}\textbf{a}}=1, \ \sqrt{\textbf{b}^TC_{yy}\textbf{b}}=1$

同样最后转化为求特征值和特征向量的问题。

PLSR(偏最小二乘回归)

•目的：用自变量中与因变量最相关的“典型变量”做回归

•因变量Y和自变量X（都已标准化）

$Y=\left[ \begin{matrix} y_1\ y_2\ \cdots\ y_q \end{matrix} \right],\ \ \ \ \ \ X=\left[ \begin{matrix} x_1\ x_2\ \cdots\ x_p \end{matrix} \right]$

•记典型变量u，v，分别是X各变量和Y各变量的线性组合

•要求

u,v的方差最大（PCA思想）

$Var(u)=\frac{\textbf{a}^TX^TX\textbf{a}}{n-1}=\textbf{a}^TC_{xx}\textbf{a}\\ Var(v)=\frac{\textbf{b}^TY^TY\textbf{b}}{n-1}=\textbf{b}^TC_{yy}\textbf{b}$

使得u,v相关性最大（CCA思想）

$Corr(u,v)=\frac{\textbf{a}^TC_{xy}\textbf{b}}{\sqrt{\textbf{a}^TC_{xx}\textbf{a}}\sqrt{\textbf{b}^TC_{yy}\textbf{b}}}$

•问题提炼为

$maximize(\textbf{a}^TC_{xy}\textbf{b})\\ 约束条件：\textbf{a}^T\textbf{a}=1,\ \textbf{b}^T\textbf{b}=1$ PLS是PCA和CCA的结合的说法是网上看到的（老师也这么讲）。但有个问题是：既然给定了样本，X和Y的协方差矩阵相当于就是固定的，那最后这个求解模型的约束条件不就和CCA是一样的？事实上就是求了个典型相关变量？

•得到了“典型变量”之后，建立Y对u1的回归，X对u1的回归

$Y =\beta_1u_1+\epsilon_{y1} \\ X =\alpha_1u_1+\epsilon_{x1}$

•用余项（$\beta_1u_1$和$\alpha_1u_1$解释后的残余信息）再建立对u2的回归

$\epsilon_{y1} =\beta_2u_2+\epsilon_{y2} \\ \epsilon_{x1} =\alpha_2u_2+\epsilon_{x2}$

•如此重复只要达到满意的精度就可以停止，得到

$Y =\beta_1u_1+\beta_2u_2+...\beta_ku_k+\epsilon \\$

•代入u的定义式

$u_1=X\textbf{a}_1,\ u_2=X\textbf{a}_2,\ ...u_k=X\textbf{a}_k$

就可以得到最终的偏最小二乘回归方程

$Y =\theta_1x_1+\theta_2x_2+...\theta_kx_k+\epsilon \\$

参考

知乎学弱猹回归分析笔记