拉格朗日乘子法

拉格朗日乘子法（Lagrange Multiplier Method）是求解带约束条件的极值问题最常见的方法之一，以大数学家Joseph Lagrange的名字命名。

首先回忆一下几个基础的概念：法向量，方向导数，梯度。

法向量（Normal Vector）

法向量最常见到的使用场景是在三维空间，直观的几何意义就是：垂直于一个平面的向量。

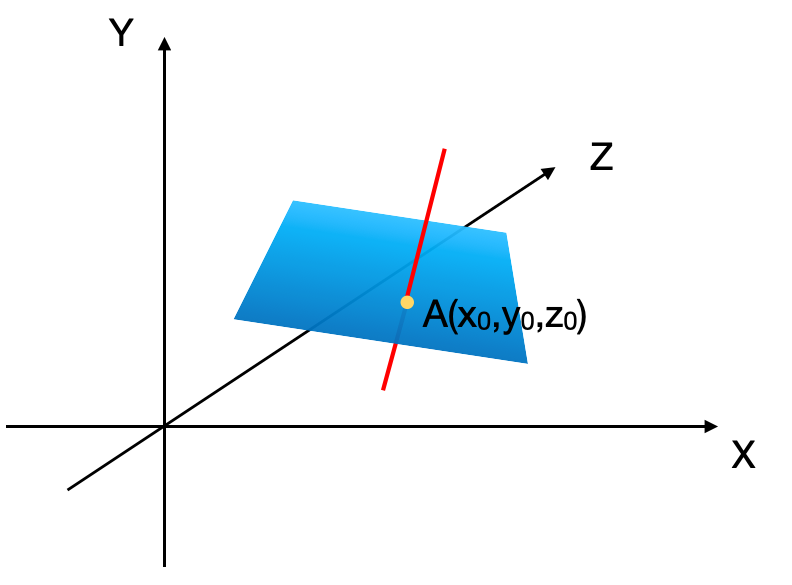
设蓝色平面上有一点A，过A点该平面的法向量为$\omega(\omega_1,\omega_2,\omega_3)$，根据法向量的定义，该平面上任意一点B与A点连线组成的直线应与$\omega$垂直。所以有：

$$\omega^T\vec{AB}=0 \\ 或 \ \omega_1(x-x_0)+\omega_2(y-y_0)+\omega_3(z-z_0)=0$$

分量形式还可写为：

$$\omega_1x+\omega_2y+\omega_3z-(\omega_1x_0+\omega_2y_0+\omega_3z_0)=0$$

事实上，这就是一个平面的定义式。一个平面可由其法向量和离开原点的距离确定，在n维空间，一个超平面的标准定义式写为：

$$f(\textbf{x})=\omega^T\textbf{x}+\textbf{b}=0$$

其中${\omega}(\omega_1,\omega_2…\omega_n)$是n维法向量，决定超平面的方向，$\textbf{b}$决定超平面离开原点的距离。

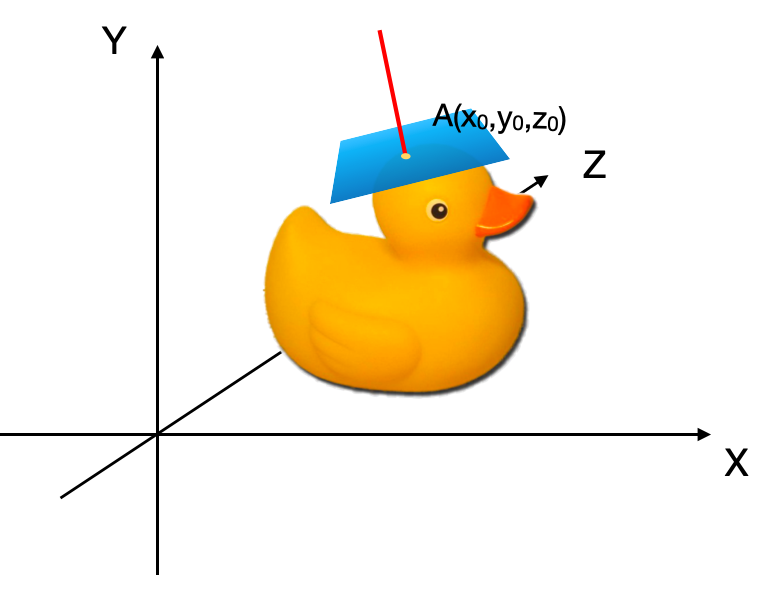
对于曲面上一点，法向量为该点所在切平面的法向量。

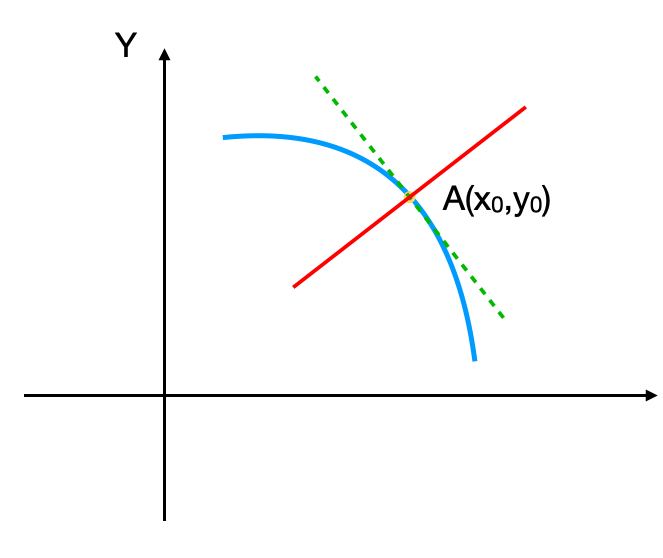
当维度减少到最小的二维时，一条直线的法线就是该直线的垂线，曲线上一点的法线就是该点处切线的法线。

反过来，知道了一个平面的方程，也可以求得法向量。对f求偏导就可以了：

$$\omega = (\frac{\partial f}{\partial x_1},\frac{\partial f}{\partial x_2},...\frac{\partial f}{\partial x_n})$$

这里有一点需要特别提醒，法向量是一个向量，向量只有一个朝向，但其实一个法向量的反向向量也是法向量。所以$-\omega$也是该平面的法向量。法向量总是对偶出现，一条法线，两个法向量（不考虑向量的大小）。这和梯度很不一样，下面将解释是什么造成了这种差别。

方向导数（Directional Derivative）

同样从三维空间开始来引入方向导数的概念。对于三维空间中的任一个面

$$z=f(x,y)$$

如下图所示

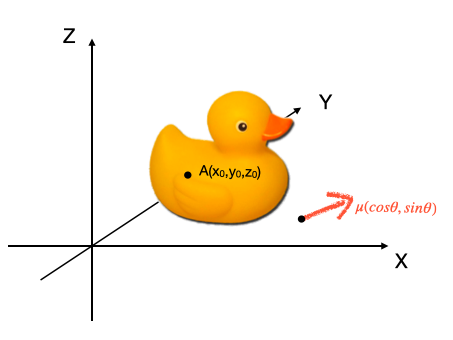
方向导数的定义为目标函数在某一方向上的变化率。

具体到我们的小黄鸭函数z=f(x,y)，z是目标函数、因变量；x,y是自变量。因为自变量只有两个维度，所以这里的“方向”一定是在二维平面上的。我们用单位向量$\mu$来表示“某一方向”，则z=f(x,y)在$\mu$方向上的方向导数定义为：从某一点（假设为A）出发，沿$\mu$方向走t长度（t趋于无穷小）后，函数值z的变化。

$$\begin{aligned} \frac{df(x_0,y_0)}{dt}&=\lim_{t \to 0}\frac{f(x_0+tcos\theta,y_0+tsin\theta)-f(x_0,y_0)}{t}\\&=f_x(x_0,y_0)cos\theta+f_y(x_0,y_0)sin\theta\\ &=(f_x(x_0,y_0),f_y(x_0,y_0))·\mu \end{aligned}$$

其中$f_x,f_y$为f对x,y的偏导数。

梯度（Gradient）

知道了方向导数是什么，梯度的概念就顺水推舟了。梯度是一个向量，它指向目标函数值增大最快的方向。

由方向导数$\frac{df(x_0,y_0)}{dt}=(f_x(x_0,y_0),f_y(x_0,y_0))·\mu$知，当$\mu$的方向与$(f_x(x_0,y_0),f_y(x_0,y_0))$的方向相同时，方向导数最大，函数值增长最快。所以梯度的定义为

$$\nabla f=(\frac{\partial f}{\partial x},\frac{\partial f}{\partial y})$$

拓展到n维，$z=f(x_1,x_2,…x_n)$

$$\nabla f=(\frac{\partial f}{\partial x_1},\frac{\partial f}{\partial x_2},...\frac{\partial f}{\partial x_n})$$

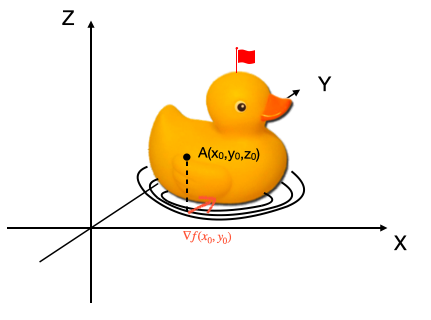
看起来，梯度和法向量的式子是一样的？梯度就是法向量？

这两个概念有一个重要的区别。同样的小黄鸭，法向量是一个三维的向量，而且一正一反有两个，而梯度却是一个二维的向量，且方向只有一个。这是为什么？关键的区别在于函数f。我们求法向量时的函数f是一个隐函数，形式为$f(x,y,z)=0$，而求梯度时f却是显函数，形式为$z=f(x,y)$。后者意味着我们有一个“目标”，根据梯度的定义，使这个“目标”更大决定了梯度只能有一个方向。而没有“目标”的法向量表示，两头都可以，只要垂直就完事了。

拉格朗日乘子法（Lagrange Multiplier Method）

等式约束条件下的极值问题

拉格朗日乘子法用来解决带约束条件的极值问题。在二维平面中举个简单的例子，假设我们的目标函数是f(x,y)，在约束$g(x,y)=0$的条件下，要求f(x,y)的最小值。

$$min\ f(x,y)\\ s.t. g(x,y)=0$$

不妨设$f(x,y)=x²+y²$，$g(x,y)=0$是如下图的一条蓝色曲线

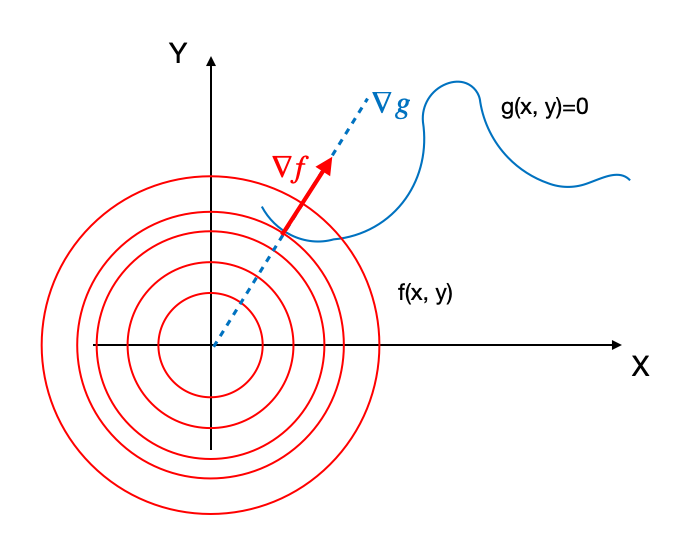
红色的圈圈是我们目标函数$z=f(x,y)$的等高线，由约束条件，只允许点(x,y)在$g(x,y)=0$上滑动。可以直观地看出，当红圈和蓝线相切时，圆的半径最小，也就是f(x,y)最小。相切也意味着，切点处红圈的梯度$\nabla f$与蓝线的法向量$\nabla g$在同一条直线上。

于是，加入了新条件的方程组为：

$$\left\{ \begin{array}{lr} \nabla f=\lambda\nabla g & \\ g(x,y)=0& \end{array} \right.$$

这里的$\lambda$就是拉格朗日乘子。

或者改写为另一种形式，构造拉格朗日函数$\mathcal{L}(x,y,\lambda)=f(x,y)+\lambda g(x,y)$，则上面的方程组等价于

$$\nabla \mathcal{L}=0$$

写开就是

$$\left\{ \begin{array}{lr} \frac{\partial \mathcal{L}}{\partial x}=0 & \\ \frac{\partial \mathcal{L}}{\partial y}=0 & \\ \frac{\partial \mathcal{L}}{\partial \lambda}=0 & \end{array} \right.$$

对于有多个限制条件的情况

$$min\ f(x,y)\\ s.t. g(x,y)=0,\ h(x,y)=0$$

目标函数的梯度是约束条件法向量的线性组合：

$$\left\{ \begin{array}{lr} \nabla f=\lambda\nabla g+\mu \nabla h & \\ g(x,y)=0& \\ h(x,y)=0& \end{array} \right.$$

不等式约束条件下的极值问题

对于有不等式约束下的条件极值问题，为了讨论的方便，我们统一形式为：

$$min\ f(x,y)\\ s.t. h(x,y)\leq 0$$

考虑可行域$h(x,y)\leq 0$，作用在$f(x,y)$上有两种情况。

1）$f(x,y)$的无约束最优解本身就在可行域内，这时约束条件无效；

2）约束条件有效，$f(x,y)$的最优解在可行域边界$h(x,y)=0$处。如下图：

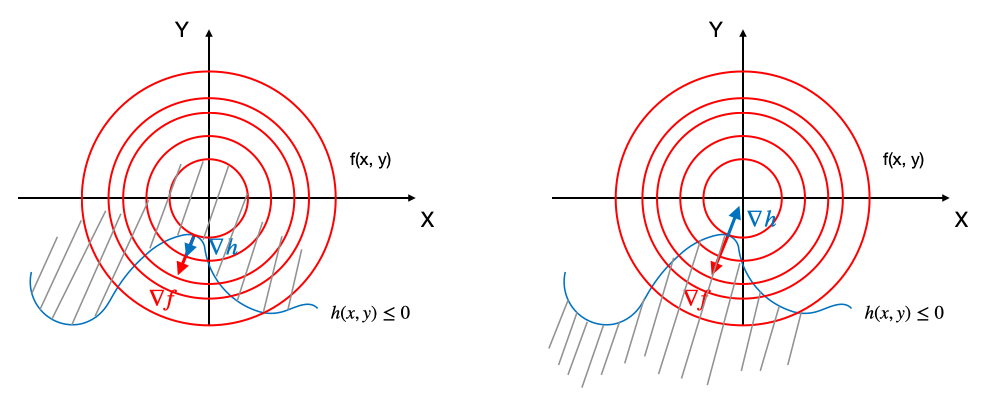
对于情况1），方程组可列为

$$\left\{ \begin{array}{lr} \nabla f=0 & \\ h(x,y)\leq 0（可忽略）& \end{array} \right.$$

对于情况2），由于我们规定了不等式约束的形式为$h\leq 0$，所以边界处的梯度$\nabla h$总是朝向可行域外部；而目标函数$f$的梯度$\nabla f$则朝向可行域内部（假如朝向外部，就变为了情况1）。所以当$f(x,y)$与可行域边界$h(x,y)=0$相切时，切点处$\nabla f$和$\nabla h$一定方向相反。

这时问题转化为等式约束条件下的极值问题，只不过增加了一个条件：

$$\left\{ \begin{array}{lr} \nabla f+\mu \nabla h=0 & \\ h(x,y)=0& \\ \mu\geq0& \end{array} \right.$$

综合情况1）和2），再加上等式约束，推广到多个约束条件，就得到了KKT条件（Karush–Kuhn–Tucker conditions）

$$\left\{ \begin{array}{lr} \nabla f+\sum_\limits{i=1}^m\lambda_i \nabla g_i+\sum_\limits{j=1}^n\mu_j \nabla h_j=0 & \\ g_i=0& \\ h_j\leq0& \\ \mu_j\geq0& \\ \mu_j h_j=0& \end{array} \right.$$

写成拉格朗日函数的形式，$\mathcal{L}(\mathcal{x},\mathcal{\lambda},\mathcal{\mu})=f(\mathcal{x})+\mathcal{\lambda}^Tg(\mathcal{x})+\mathcal{\mu}^Th(\mathcal{x})$，第一个方程变为只对拉格朗日乘子外的自变量求偏导等于0：

$$\left\{ \begin{array}{lr} \nabla_x \mathcal{L}=0 & \\ g_i=0& \\ h_j\leq0& \\ \mu_j\geq0& \\ \mu_j h_j=0& \end{array} \right.$$

参考

[直观理解梯度，以及偏导数、方向导数和法向量等]-shine-lee

[如何理解拉格朗日乘子法？]-马同学