AI学习笔记--监督学习

Logistic Regression，Naive Bayes，SVM，Decision Trees，KNN，Random Forest，Ada Boost

不涉及一些方法背后繁复的数学推导，只求列出要领。

Logistic Regression（逻辑回归/对数几率回归）

一般的线性回归模型形式为

$$f(\textbf{x})=\omega^T\textbf{x}+b$$

其输出$f(\textbf{x})$的值域是一个连续的实数域。但如果我们想要预测的是一个事件发生与否，比如基于体检指标预测是否患癌症，根据大气温度、湿度、风力和压强等预测是否会下雨，这时的因变量就是一个离散的布尔变量，$f(\textbf{x})\in \{0,1\}$。

• 用于分类的逻辑回归

  这种类型的问题可以归纳为二分类问题。从一般的线性回归模型到二分类模型，我们需要一个函数，能够把因变量从连续的实数值域映射到{0,1}值域。阶跃函数正是这样一种函数，比如，我们可以规定

  $$y=\left\{ \begin{array}{lr} 0, \ f(\textbf{x})<0 & \\ 1, \ f(\textbf{x})\geq0 & \end{array} \right.$$

  对于原函数$f(\textbf{x})$，我们还可以稍作变换，找到一个跟阶跃函数很像的”连续版本“——Sigmoid函数

  $$y=\frac{1}{1+e^{-z}}$$

  这里$z=f(\textbf{x})$。Sigmoid函数的图像为

  

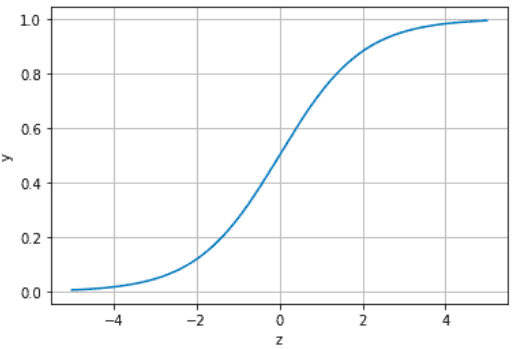
  可以看出，其值域为(0,1)，而且在y=0.5附近很陡峭。正是得益于此特性，某种程度上，Sigmoid函数的y可以看作事件发生的概率。当$y> 0.5$时，认为事件发生概率大于不发生的概率，分类为1；$y<0.$5时，反之，分类为0（这也对应一个阶跃函数）。

  Sigmoid的反函数为：

  $$z = ln\frac{y}{1-y}$$

  通常把$\frac{y}{1-y}$称为“胜算”或“几率”。

• 求逻辑回归的回归系数

  逻辑回归的回归系数用极大似然法求解，似然的概念在朴素贝叶斯方法里有简要介绍。

  假设我们的训练集为$\{(\textbf{x}_1,d_1),(\textbf{x}_2,d_2)…(\textbf{x}_m,d_m)\}$，为了区分二值的分类结果和Sigmoid函数的事件“概率”，这里分类结果记作$d_i$。回归模型为

  $$z=\omega^T\textbf{x}+b$$

  则回归模型的对数似然为

  $$L(\omega,b;(X,D))=\sum_{i=1}^mP(d_i|\omega,b;\textbf{x}_i)$$

  其中$P(d_i|\omega,b;\textbf{x}_i)$可以根据Sigmoid函数求得。

  $$P(d_i|\omega,b;\textbf{x}_i)=d_iy_i+(1-d_i)(1-y_i)$$

  最大化对数似然，求得回归系数$\omega,b$。

Naive Bayes (朴素贝叶斯)

• Bayes Rule（贝叶斯规则）

  $$P(A|B)=\frac{P(B|A)P(A)}{P(B)}$$

  分子部分P(B|A)，P(A)为先验概率，要求的P(A|B)是已知B发生的情况下A的后验概率。

• 贝叶斯规则用于分类

  从训练样本中估计先验概率，利用贝叶斯规则对测试样本分类，这种分类方法被称为贝叶斯分类器（Bayse Classifier）。

  贝叶斯公式运用到分类时具体为

  $$P(label|features)=\frac{P(features|label)P(label)}{P(features)}$$

  这里label是我们想要的分类结果，features是样本所具有的一些特征。$P(label)$是先验概率，$P(features|label)$是label条件下的类条件概率（class-conditional probability），$P(features)$用于归一化，与分类标签无关。

  贝叶斯分类的关键是如何从训练数据中估计$P(label)$和$P(features|label)$。

  对于$P(label)$，可以简单地根据大数定律估计：

  $$P(label)=\frac{D_{label}}{D}$$

  其中$D$是总的样本数，$D_{label}$是分类为label的样本数。

  然而要估计$P(features|label)$却没那么简单，这是所有特征的联合概率。而特征往往有很多个，假设每个特征都是二值的，总共有d个特征，则对于一个样本来说它的特征就有$2^d$个可能取值。不幸的的是，样本数往往比$2^d$要小，也就意味着有很多的可能取值会因为样本数不足而没有机会出现。所以，以大数定律粗暴估计就不可取。

  解决办法有两个，一个是参数估计，另外一个是假设特征条件独立。

  • 参数估计（极大似然估计）

  先简单了解一下什么是似然（Likelihood)。似然和概率可以说是一对互为逆反的双生子。一般情况下，我们知道一个概率分布，去估计某一具体事件发生的可能性，这时用到的是概率；但还有些时候，我们知道的是一些事件的结果，反过来要去推断概率分布的参数，这时用到的就是似然。

  n个独立同分布的样本$X(x_1,x_2…x_n)$，其似然是

  $$L(\theta;X)=\prod_{i=1}^nP(x_i|\theta)$$

  在对$P(features|label)$的估计中，我们先假定样本集$D_{label}$具有某种概率分布，然后令该分布的参数之似然函数（或对数似然）最大，得到的就是该种分布其参数的最优估计。这种方法称为极大似然估计。

  • 朴素贝叶斯分类

  另外一种克服直接估计$P(features|label)$困难的方法是，假设每种特征对分类的影响是独立的，即“属性条件独立性假设”（attribute conditional independence assumption）。有了这个假设，$P(features|label)$就可写开成为：

  $$P(features|label)=\prod_{j=1}^dP(f_j|label)$$

  其中$features(f_1,f_2…f_d)$有d个。这时，每个$P(f_j|label)$就可以用频率来估计了：

  $$P(f_j|label)=\frac{D^{f_j}_{label}}{D_{label}}$$

  最早朴素贝叶斯算法被用于语词分类，它无法顾及语词（每个语词是一个feature）的顺序和连用，就是因为假设每个特征之间是独立的。

Surpport Vector Machine（支持向量机）

• SVM原理

  找到一个超平面（hyperplane）或决策边界（decision boundary），能将样本最优分类。距离超平面最近的样本点被称为“支持向量（Support Vector）”，两个异类支持向量到超平面的距离之和称为间隔（margin）。SVM希望令间隔最大，这可以转化为一个有不等式约束条件的极值问题，用拉格朗日乘子法解决（KKT条件）。

  

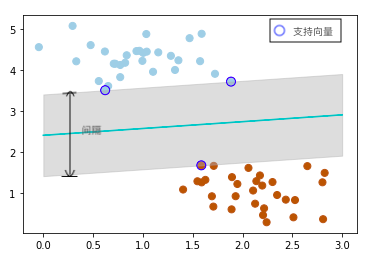
• SVM用于分类

  • 硬间隔与软间隔，MMC（Maximum Margin Classifier）与SVC（Support Vector Classifier）

  在认识什么是SVM之前，先了解一下两个概念：MMC（Maximum Margin Classifier）与SVC（Support Vector Classifier），它们是SVM的基础。

  在SVM思想刚刚提出的时候，把所有样本分类正确是必须的要求，其次才是使得间隔最大。这种分类器称为Maximum Margin Classifier（MMC）。这样严格的要求限制了其应用的场景，只有非常理想的线性可分的数据集才能使用。当找不到一个超平面划分数据集时，MMC认为出现了异常值（outlier)。

  

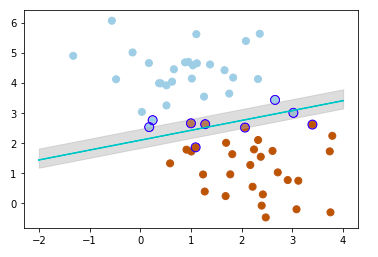
  SVC则可以容忍个别异常值，允许有个别样本点在分类边界的错误一侧。区别于严格将所有样本分类正确，这时的间隔称为软间隔（soft margin），前者当然就是硬间隔（hard margin）。简单来说是在最小化目标函数时，额外考虑边界将样本分类错误的惩罚，在原来的严格的不等式约束前加一个惩罚系数C，C越大，对样本分类正确性的要求就越严格。这样就引入了一些“弹性”，从“硬间隔”变成了“软间隔”。

  • 核技巧

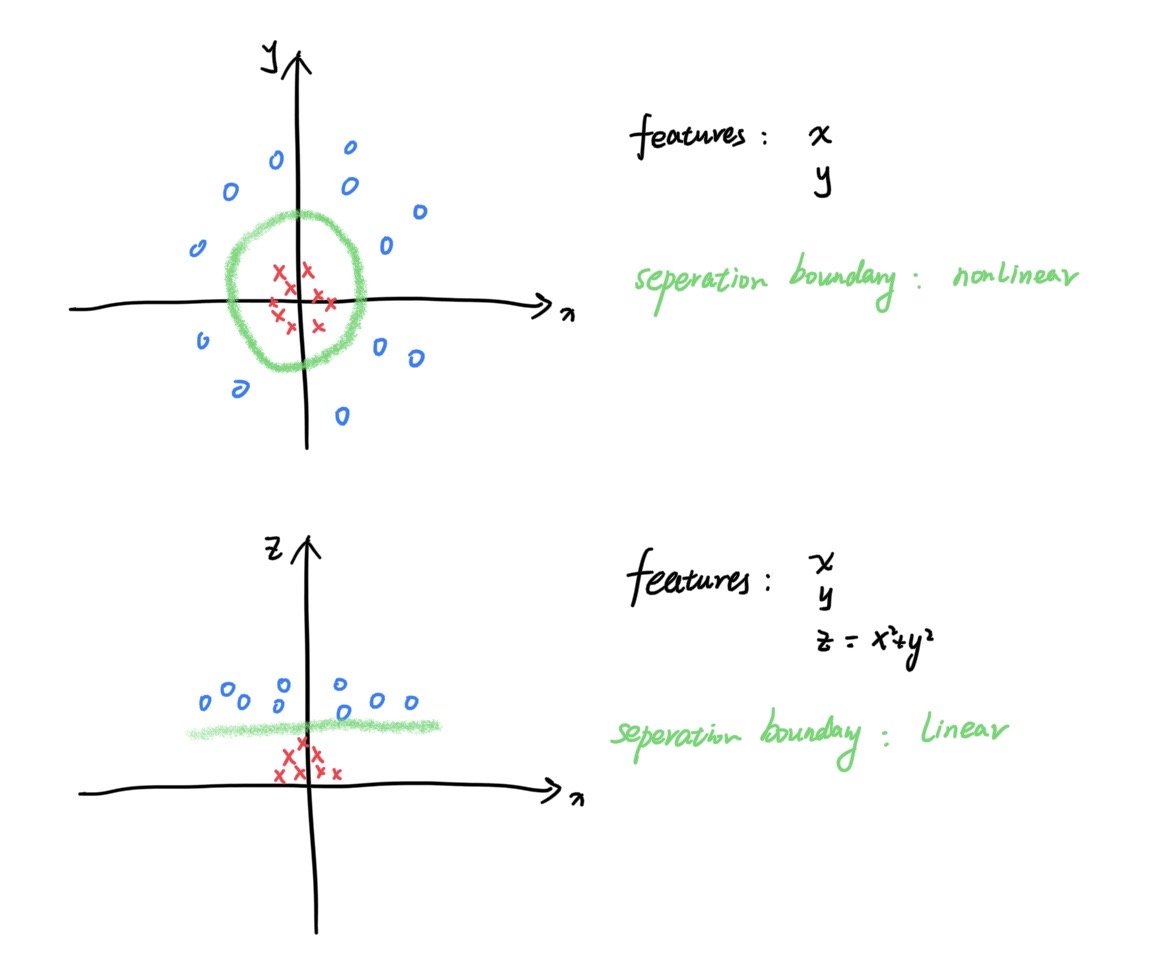
  当在原始输入的特征空间内不能找到一个线性的超平面来分割时，用到核技巧（kernel trick），把原始低维的特征映射到高维，找到一个线性超平面，再在原始特征空间表示出来。用一个最简单的例子来直观感受一下：

  

  在高维的特征空间用拉格朗日乘子法求解问题时会遇到一个困难。在原始特征空间内，不等式约束的极值问题转化为拉格朗日函数的对偶问题后，约化后求解需要计算$x_i^Tx_j^T$，而转化到高维特征空间，这个式子就变策成了$\phi(x_i)^T\phi(x_j)$，其中$\phi(x)$是$x$映射到高维特征空间的向量。当$\phi(x)$所在空间的维数很高时，不可能对$\phi(x_i)^T\phi(x_j)$直接计算。但是假如我们知道一个函数$\kappa(x_i,x_j)=\phi(x_i)^T\phi(x_j)$，就可以直接在原始特征空间计算高维特征空间的内积。这个$\kappa(x_i,x_j)$函数就称为核函数（kernel function）。

  实际中，我们不是先知，核函数的具体形式我们是不知道的，只能靠猜。所以核函数的选择是SVM一个非常大的不确定性因素。

  SVM可以用于多分类吗？

• SVM用于回归

  SVM也可以用来处理回归问题。传统的回归问题是最小化模型输出$f(x)$样本真实值$y$之间的差距。SVM回归的区别在于它可以容忍$f(x)$和$y$之间有$\epsilon$的偏差，小于$\epsilon$的偏差忽略不计入损失。相当于以$f(x)$为中心，构建了一个宽度为$2\epsilon$的间隔带，落入此间隔带的样本都被认为是预测正确的。

Decision Trees（决策树）

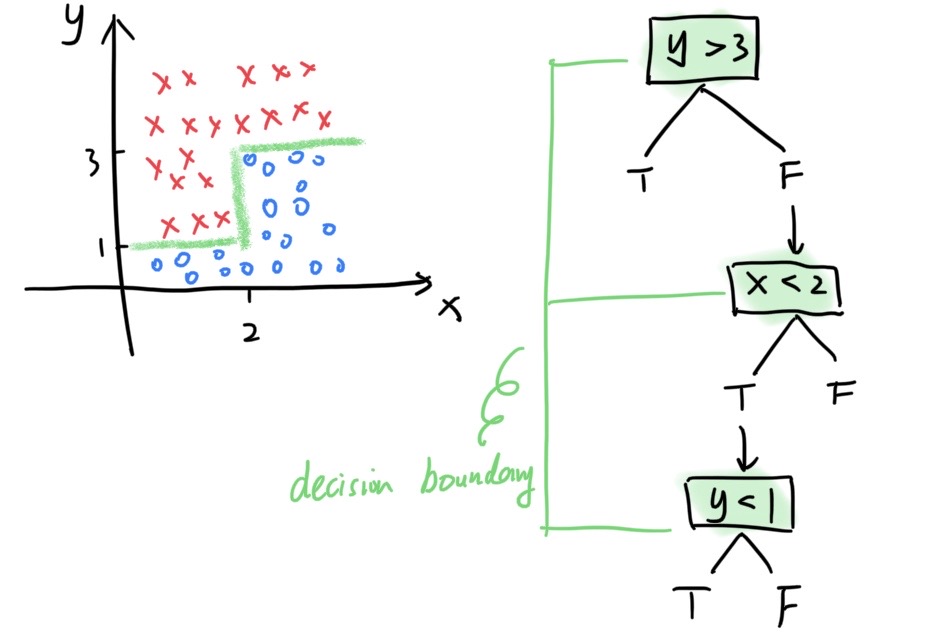
面临一个多元线性问题时，决策树可以找到一个“锯齿状”的边界。这是决策树边界的一个最明显的特征。决策树算法就是用计算机找到最合适的这种边界。它从训练集中得到一个树状模型，包含一个根节点，若干内部节点和叶节点。每个分支节点都是一次决策，这样一系列的决策决定了我们的最终分类判断。

• Entropy（熵）

  熵（Entropy）用来衡量一类中样本的杂质含量（impurity）。公式为：

  $$Entropy(D) = \sum\limits_{i}^{|\textbf{y}|}{-P_i}log_2P_i$$

  其中$P_i$是当前样本集D中第i类的样本所占的比例，$|\textbf{y}|$是类别数。当所有样本均为同一类时，纯度最高，Entropy=0；当各类样本在样本集中均匀分布时，杂质含量最高，$Entropy = log_2|\textbf{y}|$。

  一种更本质的理解是，熵是不确定性的度量，写成$Entropy = \sum\limits_{i}{P_i}log_2\frac{1}{P_i}$，$log_2\frac{1}{P_i}$是第i类的不确定程度/混乱程度。机器学习算法想要从海量数据（经验）中获得确定性的信息（模型），就如同沙里淘金。当沙子和金子混在一起时，纯度很低，熵很高；当沙子和金子清楚地分成两堆，这时纯度就很高，熵就很低。纯度很高的金子就是我们想要的确定性的信息，沙子则是噪音。

• Information gain（信息增益）

  如何把金子从沙堆里淘出来呢？现在我们有了评价金子纯度的方法——熵，要想办法让熵越小越好，这样金子的纯度就越高。决策树就是依次选择最优的特征进行划分，能让熵减小得越多的划分方法，就是越好的划分。信息增益（information gain）就是评价“熵减小”量的一个指标。

  决策树划定决策边界的依据，也就是决策树算法的核心，是要最大化信息增益。用特征a对样本集D划分的信息增益为：

  $$information\ gain(D,a)=Entropy_{parent}(D)-\sum\limits_{v}^{V}\frac{|D^v|}{|D|}Entropy_{children}(D^v)$$

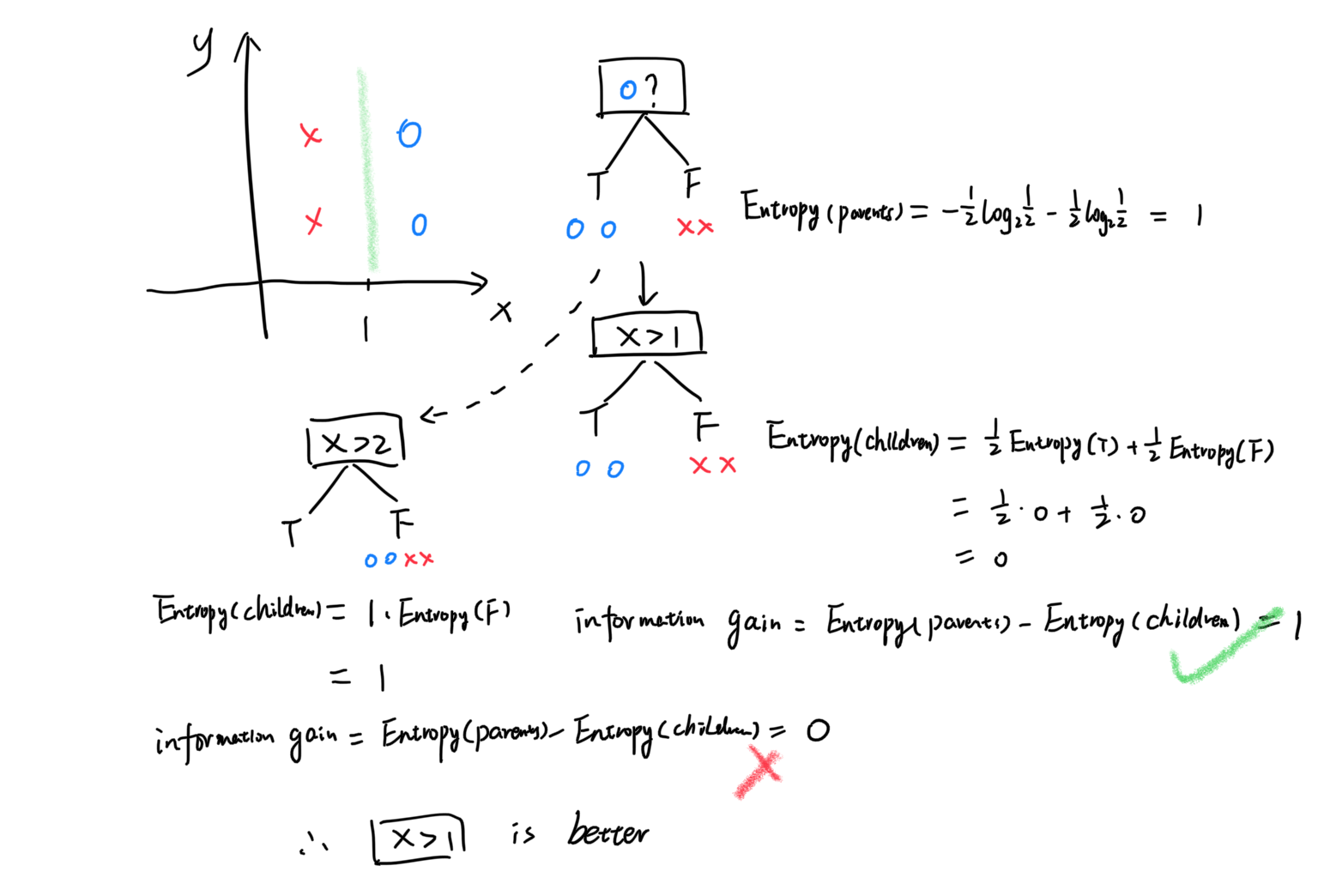
  其中特征a共有V个可能取值，取值为$a^v$的样本子集包含的样本数为$|D^v|$。在上一层划分的基础上，如何决定下一个分支节点用哪个特征进行划分，需要用到信息增益。举个例子：

  

  假如我们想把样本集分为两类：蓝圈和红叉。根节点是样本全集。计算出根节点的信息熵为1。下面要决定下一个分支节点选用哪个特征进行划分，这里拿特征$x>1$和$x>2$举例。比较信息增益得知，前者更适合作为下一个分支节点。

  以信息增益作为判别标准的算法称为ID3（Iterative Dichotomiser）。信息增益有一个缺点，它对可能取值数多的特征有偏好。同样是在各特征取值均匀分布情况，特征可能取值数多的，信息增益会更大。为了克服这个缺点，改进的C4.5算法是以增益率作为标准。后来的CART决策树是以基尼指数（Gini index）作为标准。

K-Nearest Neighbors（K最邻近）

Random Forest（随机森林）

Ada Boost

选择算法

1）理解算法原理，适合哪种数据

2）用测试集检验算法的表现

参考

[机器学习入门]-udacity

[机器学习西瓜书]-周志华

[机器学习算法（AI入门体验）开源学习资料]-Datawhale

[决策树算法原理]-刘建平

[Road to SVM: Maximal Margin Classifier and Support Vector Classifier]-Valentina ALto