AI学习笔记--强化学习

强化学习在“机器”与“环境”的交互中完成。机器对环境采取一个动作（Action），环境状态（State）会相应作出改变；环境状态的变化对应了一个奖励（Reward），来反馈给机器。强化学习要解决的问题就是：为机器找到一个最优的策略（Policy），这个策略对应的动作序列使得长期累积的奖赏最大。

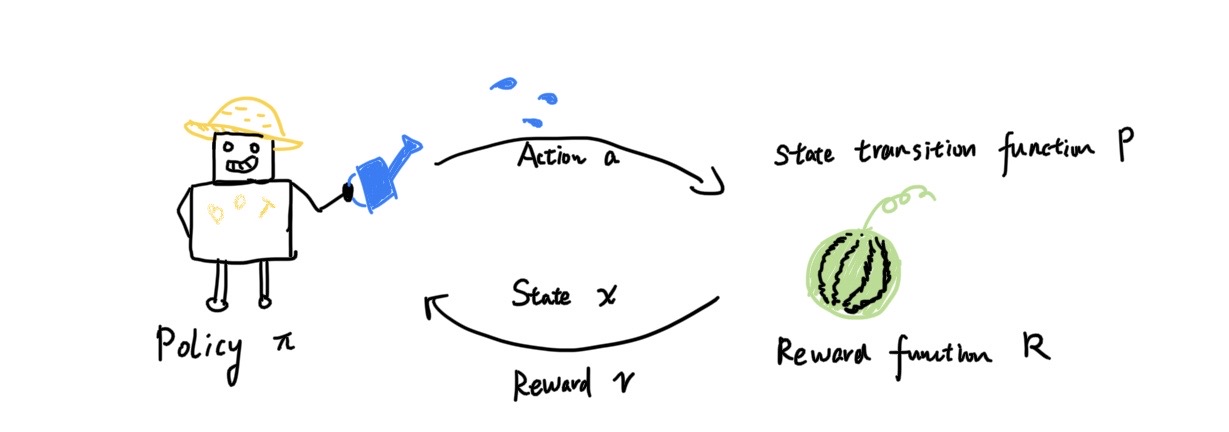
• 监督学习：样本已标记；样本独立（IID，独立同分布）

• 强化学习：延迟标记（奖励）；样本通常是序列

序列决策（Sequential Decision Making）

选择一个动作序列，使得这个动作序列获得总的奖励最大。奖励可能是即时的，也可能是延迟获得的。

History：由观测、动作、奖励构成的序列

$$H_t =O_1,R_1,A_1,...A_{t-1},O_t,R_{t}$$

State：History决定了当前状态，用来决策下面的动作。

$$S_t = f(H_t)$$

环境状态和机器状态

Policy

• Deterministic

• Stochastic

第二章 马尔可夫决策过程（MDP）

1. 马尔可夫链、马尔可夫奖励过程、马尔可夫决策过程

1.1 马尔可夫链（Markov Chain）

下一时刻的状态只取决于当前时刻的状态，而与过去的历史状态无关，称为马尔可夫特征。 具有马尔可夫特征的一系列状态构成一条马尔可夫链。

1.2 马尔可夫奖励过程（Markov Reward Process）

对不同的状态s设定奖励R(s)，就形成了对某些状态的偏好。

给定一条马尔可夫链，从某一时刻t开始，到最大时步T结束，得到的总奖励值称为回报（Return）或累积奖励。常用的累积奖励形式有

$$T步累积奖励：G_t=\frac{1}{T}(R_{t+1}+R_{t+2}+...+R_T)$$ $$\gamma折扣累积奖励：G_t=R_{t+1}+\gamma R_{t+2}+\gamma^2 R_{t+3}+...$$

某一状态s在t时刻的价值函数(value function)是t时刻从该状态出发得到回报的期望

$$V_t(s)=E(G_t|s_t=s)$$

定义了价值函数，我们的目标就具象了起来：想要更多的回报，就要令价值函数越大越好。

价值函数的计算有两种方法：

• Monte Carlo采样（采样得到足够多的马尔可夫链样本，计算回报的期望）

• Bellman Equation（迭代式）

$$V(s)=R(s)+\gamma \sum_{s' \in S}P(s'|s)V(s')$$

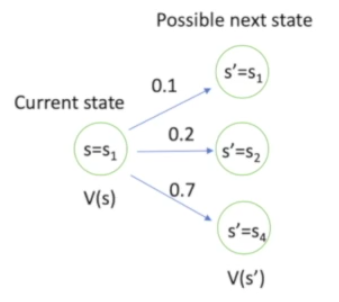
这里面的$P(s’|s)$是状态转移函数，含义是从当前状态s向下一个状态s‘转移的概率。

假设马尔可夫链无限长，即终止时间T无限大，则$V(s)=V(s’)$，Bellman equation可以写成矩阵形式

$$\left[ \begin{matrix} V{(s_1)} \\ V{(s_2)} \\ \vdots \\ V{(s_n)} \\ \end{matrix} \right] =\left[ \begin{matrix} R{(s_1)} \\ R{(s_2)} \\ \vdots \\ R{(s_n)} \\ \end{matrix} \right]+\gamma \left[ \begin{matrix} P{(s_1|s_1)}& P{(s_2|s_1)}& \cdots& P{(s_n|s_1)}\\ P{(s_1|s_2)}& P{(s_2|s_2)}& \cdots& P{(s_n|s_2)}\\ \vdots &\vdots& \ddots & \vdots\\ P{(s_1|s_n)}& P{(s_2|s_n)}& \cdots& P{(s_n|s_n)}\\ \end{matrix} \right] \left[ \begin{matrix} V{(s_1)} \\ V{(s_2)} \\ \vdots \\ V{(s_n)} \\ \end{matrix} \right] \\ V=R+\gamma PV$$

解析解为$V=(I-\gamma P)^{-1}R$，实际求解方法有Dynamic Programming、Monte-Carlo、Temporal-Difference learning等。

1.3 马尔可夫决策过程（Markov Decision Process）

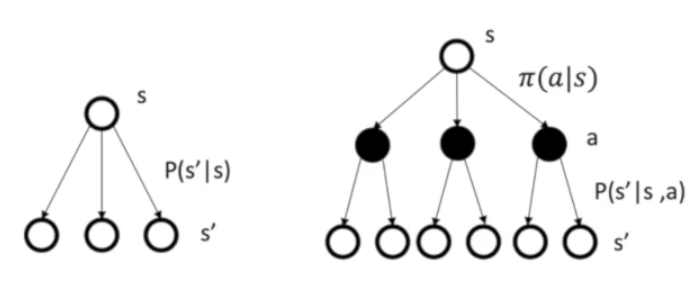
与马尔可夫奖励过程相比，马尔可夫决策过程从当前状态向下一状态的转移由动作（Action）决定。加入动作之后，MRP中状态的奖励$R(s)$在MDP里变为$R(s,a)$。这种说法其实并不严谨，当前状态的奖励怎么会除了状态本身相关，还受下一步要采取的动作影响呢？下面会解释它们之间细微的差别。

我们制定一个策略（Policy）来决定一系列动作

$$\pi (a|s)=P(a_t=a|s_t=s)$$

如果策略确定，马尔可夫决策问题就可以转化为马尔可夫奖励问题

$$P^{\pi}(s'|s)=\sum_{a\in A}\pi(a|s)P(s'|s,a)\\ R^{\pi}(s)=\sum_{a\in A}\pi(a|s)R(s,a)$$

其中$P(s’|s,a)$是转移函数（Transition function）。根据2式我们可以体会到，为什么$R(s,a)$的定义是不自然的：它是为了引入动作（确切地说是策略$\pi(a|s)$）而构造出的一个定义，可以理解为把状态s的奖励按概率$\pi(a|s)$掰开得到的一个量。

MRP（左） MDP（右）

确定策略的MDP问题已经退化为MRP问题，则可以定义类似的状态值函数（state-value function）

$$V^{\pi}(s)=E_{\pi}(G_t|s_t=s)$$

写出Bell equation

$$\begin{aligned} V^{\pi}(s)&=R^{\pi}(s)+\gamma \sum_{s' \in S}P^{\pi}(s'|s)V^{\pi}(s')\\ &=\sum_{a\in A}\pi(a|s)(R(s,a)+\gamma\sum_{s'\in S}P(s'|s,a)V^{\pi}(s')) \end{aligned}$$

我们新定义一个动作-状态值函数（action-value function）$q^{\pi}(s,a)$，令

$$q^{\pi}(s,a)=R(s,a)+\gamma\sum_{s'\in S}P(s'|s,a)V^{\pi}(s')$$

类似地，$q^{\pi}(s,a)$是把状态值函数$V^{\pi}(s)$按动作概率$\pi(a|s)$掰开得到的，它的含义是在状态s采取动作a，之后的策略仍然确定，所能获得的回报的期望。

2. 策略评估

之前提到，定义了价值函数让我们的目标具象了起来，强化学习是一个MDP过程，令价值函数最大，理论上就能得到一个最优的策略。所以，给定一个策略$\pi$，计算该策略下的价值函数$V^{\pi}$，$V^{\pi}$的大小可以反映策略$\pi$的优劣。这个过程叫策略评估（Policy evaluation）。

计算价值函数的方法我们前面也有提及，最常用的做法是利用Bellman Equation迭代至收敛

$$V^{\pi}_{t+1}(s) =\sum_{a\in A}\pi(a|s)(R(s,a)+\gamma\sum_{s'\in S}P(s'|s,a)V^{\pi}_{t}(s'))$$

这实际上就是一种动态规划算法，从$t_0$时刻出发，迭代一次得到单步奖赏$V^{\pi}_{t_1}$，继续迭代得到$V^{\pi}_{t_2},V^{\pi}_{t_3}…$，直至收敛就得到各个状态的价值函数$V^{\pi}$。这里迭代至收敛是对应$\gamma$折扣累积奖励而言的，如果是T步累积奖励则只需迭代T轮。

3. 马尔可夫决策控制

现在我们知道了怎么计算单个策略对应的价值函数（策略评估），下一步就是在众多策略中找到价值函数最大的那个（最优策略）。这一步叫马尔可夫决策控制（MDP control）。

一个最简单粗暴的方法就是穷举，把所有可能的策略都试一遍。或者写出价值函数的解析解形式，$V^{\pi}$是状态和策略的函数，理论上可以令价值函数最大求解。但这两种思路实际几乎不可操做，下面介绍更可行的方法。

3.1 策略迭代（Policy Iteration）

策略迭代使用贪心算法找最优策略。先给定一个初始策略$\pi_0$，计算价值函数$V^{\pi_0}$；下一个动作选择当前状态下的最优动作——即令动作-状态值函数$q^{\pi_0}(s,a)$最大；这样得到了新的策略$\pi_1=\underset{a}{\arg\max}\ q^{\pi_0}(s,a)$，再计算价值函数$V^{\pi_1}$，…迭代直至收敛。(注意这里使用的是deterministic policy)

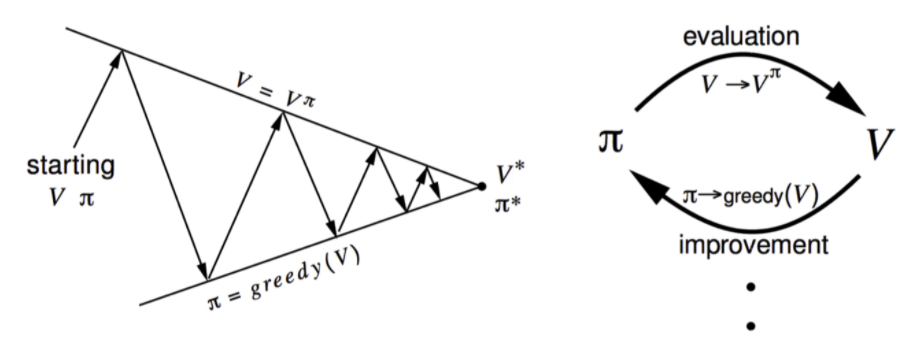
可以证明，这种贪心迭代的过程中价值函数是单调递增的，因为

$$q^{\pi_{i+1}}(s,\pi_{i+1}(s))=\max_{a}q^{\pi_i}(s,a)\geq q^{\pi_i}(s,\pi_i(s))=V^{\pi_i}(s)$$

这样最终迭代收敛得到的

$$V^{*}(s)=\max_{a} q^*(s,a)\\ \pi^*=\underset{a}{\arg\max}\ q^*(s,a)$$

就是最大价值函数和最优策略。

3.2 价值迭代（Value Iteration）

在策略迭代中，令动作-状态值函数最大来改进策略的过程

$$\pi_{i+1}=\underset{a}{\arg\max}\ q^{\pi_i}(s,a)$$

其实与改进值函数是一致的，因为我们选择determinist policy，所以值函数

$$V^{\pi_{i+1}}(s)=q^{\pi_{i+1}}(s,\pi_{i+1}(s))=\max_{a}q^{\pi_i}(s,a)\geq q^{\pi_i}(s,\pi_i(s))=V^{\pi_i}(s)$$

既然是一致的，我们就可以直接对值函数迭代，省去策略迭代里每次策略更新后都要进行的策略评估过程。用Bellman optimality equation

$$V^NaN(s)=\max_{a}q^{i}(s,a)$$

迭代值函数至收敛，然后重构出最佳策略

$$\pi^*=\underset{a}{\arg\max}\ q^*(s,a)$$

参考

[introRL-周博磊]