集合论与关系

集合的基本模型无法描述一种广泛存在的”序”的概念，因为集合中的元素是无序的。能不能在集合论的基础上描述“序”呢？

一、关系的引入

1.1 有序对

在使用集合论对“序”给出定义之前，我们先用自然一点的语言试着描述什么是“序”。设a, b为对象，我们记(a,b)为一个有序对（ordered pair），满足$(a,b)=(c,d)\Leftrightarrow (a=c \wedge b=d)$。其中a称为第一分量，b称为第二分量。

有序对的条件$(a,b)=(c,d)\Leftrightarrow (a=c \wedge b=d)$实际上规定了第一分量和第二分量是不可交换的，这就是对“序”的数学描述。1914年，Wiener第一次尝试在集合论的基础上给出了有序对的定义

$$(a,b)=\{\{\{a\},\emptyset\},\{\{b\}\}\}$$

1921年，Kuratowsk给出了另一种更简洁的定义

$$(a,b)=\{\{a\},\{a,b\}\}$$

可以证明这两种定义都满足有序对的条件。

1.2 笛卡尔积

对集合A与B，称$A\times B=\{(a,b)|a \in A\wedge b \in B \}$为集合A与B的笛卡尔积。

例如，假设$A=\{1,2,3\},B=\{a,b\}$，则$A\times B=\{(1,a),(1,b),(2,a),(2,b),(3,a),(3,b)\}$。

笛卡尔积有若干定理：

$$\begin{align} &(1)\ A\times \emptyset=\emptyset \times A = \emptyset\\ &(2)\ A \times B=B \times A\\ &(3)\ A \times (B\cup C)=(A\times B)\cup (A\times C)\\ &\ \ \ \ \ \ A\times (B\cap C)=(A \times B)\cap(A\times C)\\ &\ \ \ \ \ \ (B\cup C)\times A=(B \times A)\cup(C\times A)\\ &\ \ \ \ \ \ (B\cap C)\times A=(B \times A)\cap(C\times A) \end{align}$$

二、关系的定义

现在定义了有序对，下一步可以定义关系：关系是有序对的集合。集合R为关系指

$$(\forall r \in R)(\exists x,y)(r=(x,y))$$

设A，B为集合，若$R\subseteq A\times B$，称$R$为从A到B的二元关系。当$A=B$时，称R为A上的二元关系，在无歧义时一般简称关系。若$(a,b)\in R$，可简记为$aRb$。

2.1 空关系、全关系、恒同关系

• 空关系：$\emptyset \subseteq A \times A$

• 全关系：$E_A=\{(x,y)|x,y \in A\}$

• 恒同关系：$I_A=\{(x,x)|x\in A\}$

2.2 定义域、值域、域

定义与关系R有关的3个重要集合，设$R\subseteq A\times B$

• R的定义域：$Dom(R)=\{x|(\exists y \in B)(x,y)\in R\}$

• R的值域：$Ran(R)=\{y|(\exists x \in A)(x,y)\in R\}$

• R的域：$Fld(R)=Dom(R) \cup Ran(R)$

2.3 用矩阵或有向图表示二元关系

设$A=\{a_1,a_2…a_m\}$和$B=\{b_1,b_2…b_n\}$，$R\subseteq A\times B$为A到B的二元关系，则可用一个$m \times n$的矩阵表示关系R，关系矩阵$M_R=[m_{ij}]_{m\times n}$

$$m_{ij}= \left\{ \begin{array}{lr} 1,\ if (a_i,b_j )\in R\\ 0,\ if(a_i,b_j )\notin R \end{array} \right.$$

举个例子，$A=\{1,2,3\}$，$B=\{a,b\}$，$R=\{(1,a),(1,b),(2,a),(3,b)\}$，用矩阵表示为

$$\left[ \begin{matrix} 1& 1\\ 1& 0 \\ 0& 1 \end{matrix} \right]$$

用有向图表示为

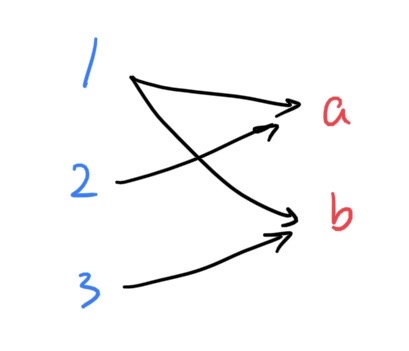
三、 关系的运算

3.1 关系的逆

设$R\subseteq A\times B$，则R的逆

$$R^{-1}=\{(y,x)|(x,y)\in R\}$$

$R^{-1}$是从B到A的关系，$R^{-1}\subseteq B \times A$。

3.2 关系的复合

设$S \subseteq A \times B,\ R\subseteq B \times C$，R与S的复合为

$$R\circ S=\{(x,y)|(\exists t \in B)((x,t)\in S \wedge (t,y)\in R)\}$$

其实就是$x(R\circ S)y \Leftrightarrow \exists t(xStRy) $。

有运算规则

$$\begin{align} &(1)\ (R^{-1})^{-1}=R\\ &(2)\ R_1 \circ (R_2\circ R_3)=(R_1 \circ R_2)\circ R_3\\ &(3)\ (R\circ S)^{-1}=S^{-1}\circ R^{-1}\\ &(4)\ I_B\circ R=R\circ I_C =R \end{align}$$

假如你熟悉线性代数里矩阵运算规则就会意识到，关系复合的运算规则和矩阵运算规则形式是一致的。回到集合论的原始观点，矩阵可以视为关系的表示，矩阵运算其实就是对关系的运算。

3.3 关系的幂

设$R\subseteq A\times A$（注意这里R是集合A到自身的关系，对应的矩阵为方阵），则归纳定义R的n次幂

$$R^0=I_A,\ R^{n+1}=R \circ R^n$$

关系的幂的朴素含义：乘一次幂就相当于多加入一个中间点。

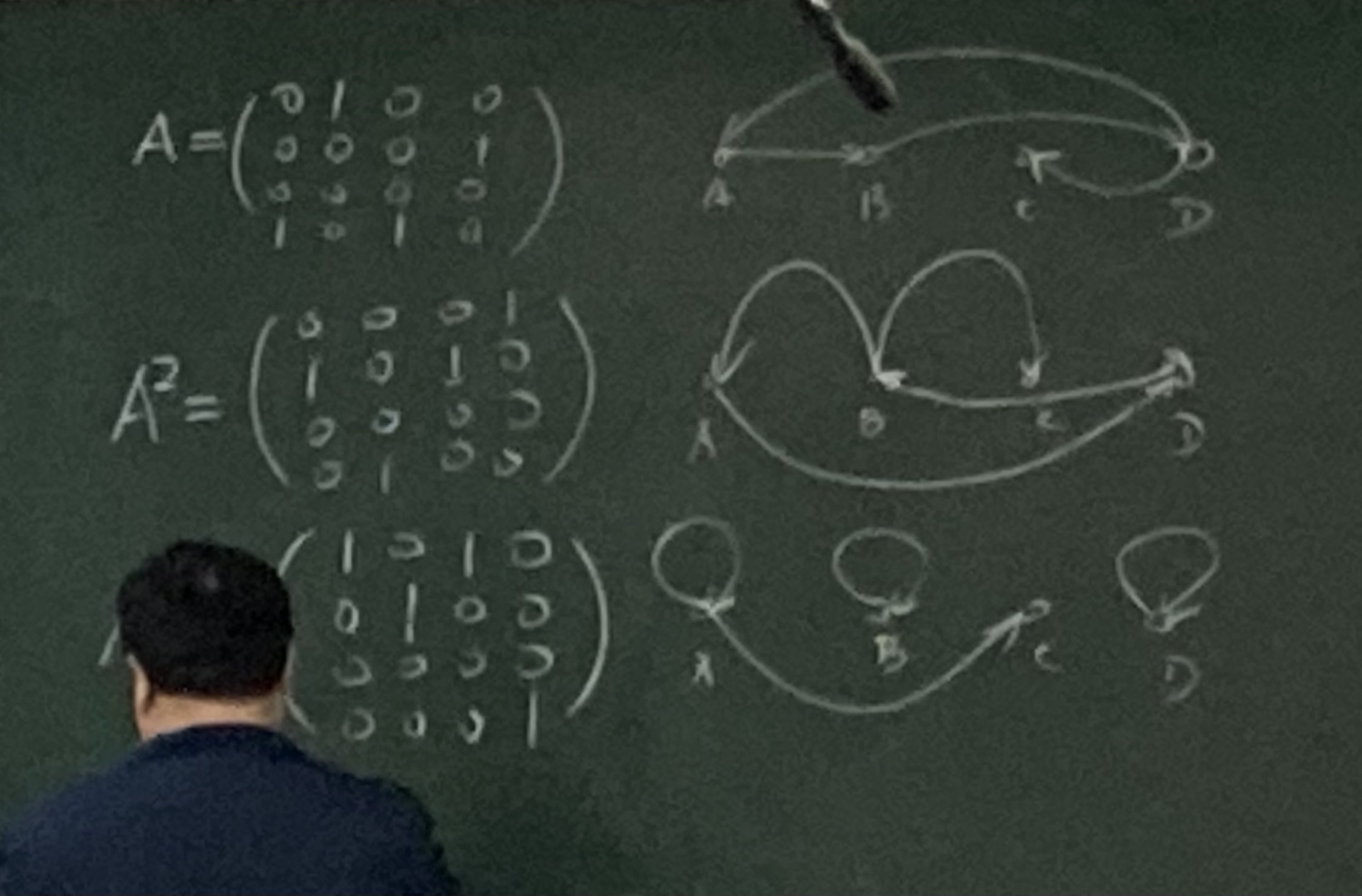
一些关于关系的幂的定理

$$\begin{align} &(1)\ R^{m}\circ R^n{=R^{m+n}}\\ &(2)\ (R^{m})^n=R^{mn}\\ &(3)\ 若\exists S\in \mathbb{N},T\in \mathbb{N}^+使R^S=R^{S+T},则\\ &\ \ \ \ \ \ a.(\forall k \geq S)(R^k= R^{k+T})\\ &\ \ \ \ \ \ b.(\forall k \geq S)(\forall n \in \mathbb{N})(R^k= R^{k+nT})\\ &\ \ \ \ \ \ c.\{R^0,R^1,...,R^{S+T-1}=\{R^0,R^1,...,R^n,...\}\}\\ &(4)\ 若|A|=n,则(\exists s,t \in \mathbb{N})(R^s=R^t \wedge 0 \leq s \leq t\leq 2^{n^2}) \end{align}$$

四、关系的性质

4.1 自反性、对称性和传递性

• 自反性

  R在A上自反（reflexive）：$(\forall x \in A)(xRx)$

  R在A上反自反（irreflexive）：$(\forall x \in A)(\neg xRx)$

  

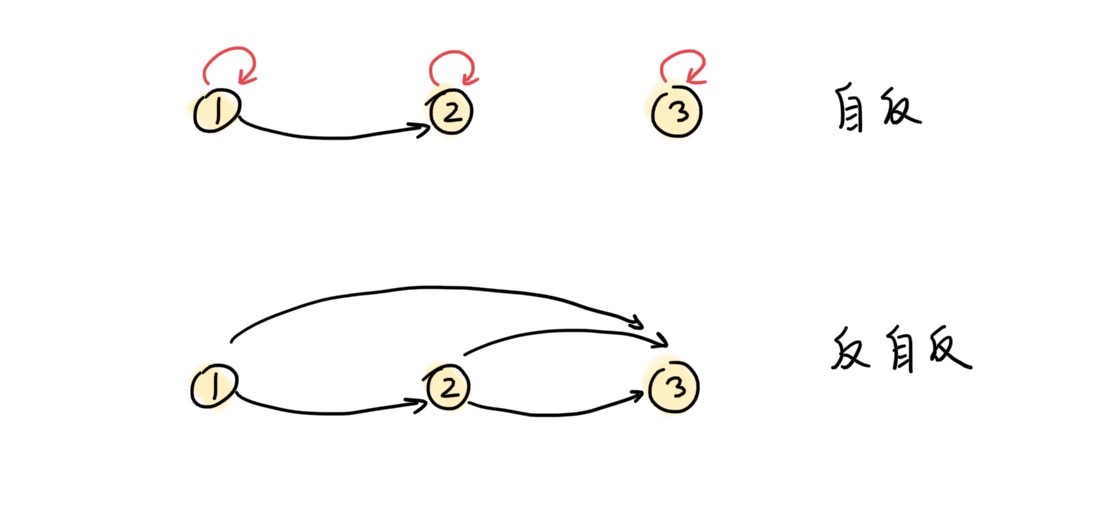
  定理：$R是A上的自反关系\Leftrightarrow I_A\subseteq R$

• 对称性

  R在A上对称（symmetric）：$(\forall x,y \in A)(xRy \to yRx)$

  R在A上反对称（anti-symmetric）：$(\forall x,y \in A)(xRyRx \to x=y)$

  R在A上强反对称（anti-symmetric）：$(\forall x,y \in A)(xRy\to \neg yRx)$

  

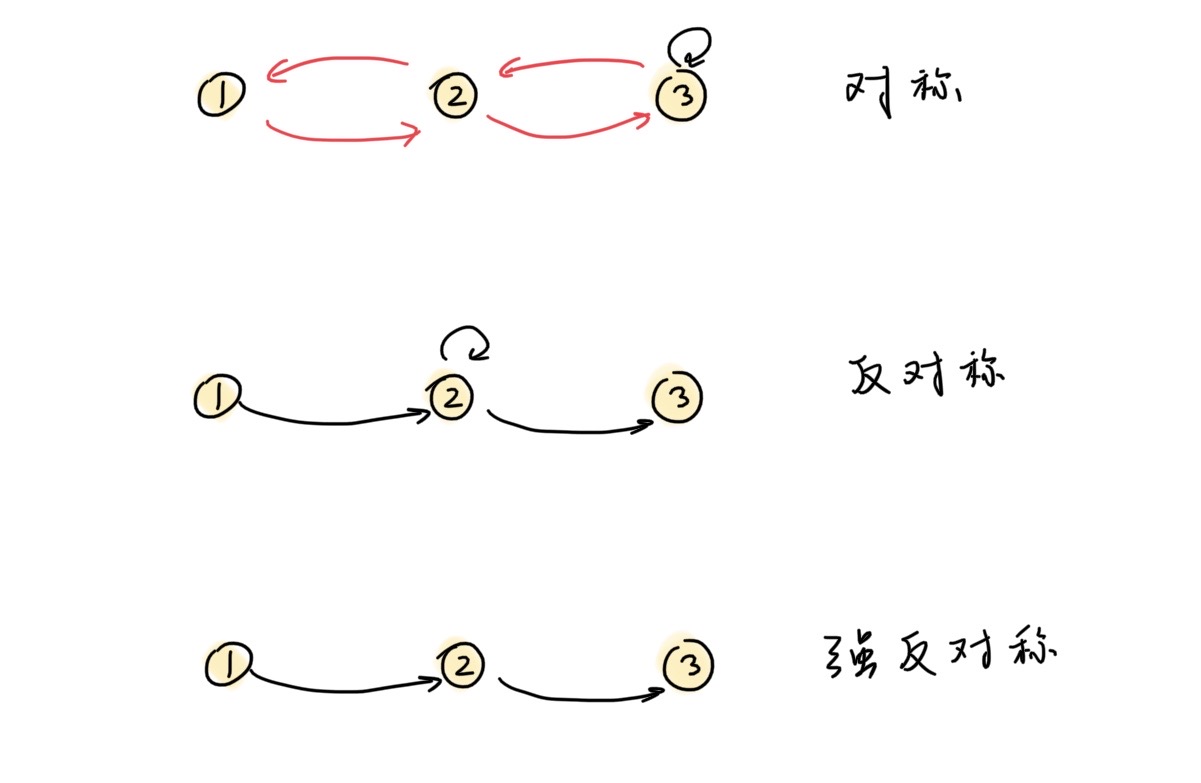
  定理：$R是集合A上的对称关系\Leftrightarrow R=R^{-1}$

  定理：$R是集合A上的反对称关系\Leftrightarrow R\cap R^{-1}\subseteq I_A$

• 传递性

  R在A上传递（transitive）：$(\forall x,y,z \in A)(xRyRz \to xRz)$

  

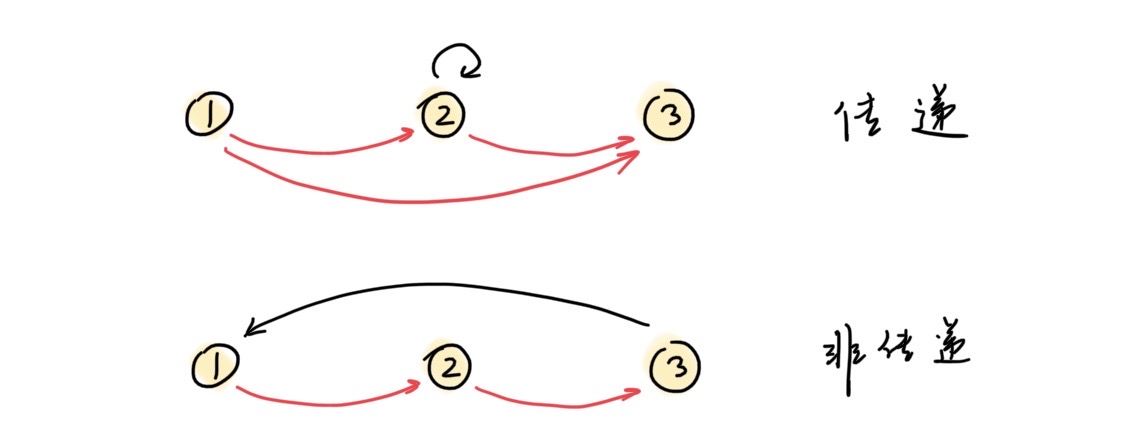
  定理：$R在A上传递\Leftrightarrow R\circ R\subseteq R$

4.2 等价关系

4.2.1 等价关系

设R为集合A上的关系，若R自反、对称且传递，则称R为A上的等价关系（equivalence relation），记为$x～ _{R}y$或$x～y$。

一个例子：整数集$\mathbb{Z}$上关于模n的同余关系为等价关系。

4.2.2 等价类

令R为A上的等价关系，对任意$a\in A$，a关于R的等价类（equivalence class）$[a]_R$

$$[a]_R\equiv \{b\in A|aRb\}$$

简记为$[a]$。

一个例子：R为整数集$\mathbb{Z}$上关于模n的同余关系为等价关系，则$[x]=\{y \in \mathbb{Z}|x \equiv y(mod\ n)\}=\{x+kn|k\in \mathbb{Z}\}$

4.2.3 商集

设R为非空集合A上的等价关系，以R的所有等价类作为元素的集合称为A关于R的商集（quotient set）$A/R$

$$A/R=\{[x]_R|x\in A\}$$

例子：设$A=\{1,2,…8\}$，A关于模3等价关系R的商集为$A/R=\{\{1,4,7\},\{2,5,8\},\{3,6\}\}$

4.2.4 集合的划分

设A为非空集合，若A的子集族$\Pi$（A的子集构成的集合）满足：

$$\begin{align} &(1)\ \emptyset \not \in \Pi \\&(2)\ (\forall X,Y\in \Pi)(X\not=Y\to X\cap Y=\emptyset)\\ &(3)\ \cup\Pi =A \end{align}$$

则称$\Pi$是A的一个划分（partition），称$\Pi$中的元素为A的划分块（block）。

对于非空集合A：

• 每个商集—唯一划分
• 等价关系—不同的划分方式

4.3 关系的闭包

设$R$为集合$A$上的关系，$P$为某个性质（自反性、对称性、传递性之一），若存在$S\subseteq A \times A$，满足

$$\begin{align} &(1)\ R \subseteq S \\&(2)\ S具有性质P\\ &(3)\ \forall T(R\subseteq T \wedge T具有性质P \to S \subseteq T) \end{align}$$

则称S为相对于P的R闭包（R的P闭包）。

定理：R的P闭包存在且唯一。

4.3.1 闭包的实用构造

设$R\subseteq A \times A$，

• R的自反闭包$r(R)=R\cup R^0=R\cup I_A$
• R的对称闭包$s(R)=R\cup R^{-1}$
• R的传递闭包$t(R)=R\cup R^2 \cup R^3\cup …=\cup \{R^n|n\in \mathbb{N}^+\}$

4.3.2 闭包的关系矩阵表示

设$R\subseteq A\times A$且$A=\{a_1,…,a_n\}$，$M_R$为R的关系矩阵，则

• $M_{r(R)}=M_R\vee M_{I_A}$

• $M_{s(R)}=M_R\vee M_R^T$

• $M_{t(R)}=M_R\vee M_R^{[2]}\vee … \vee M_R^{[n]}$，其中$M_R^{[k]}=\underbrace{M_R\odot M_R\odot …\odot M_R}_{k}$

参考

主要整理自吴楠老师《离散数学》课堂讲授