一个好的局地化函数,也是提升集合同化方法表现的一块重要拼图。
概率预报与集合卡尔曼滤波
自1969年Edward Epstein发表《Stochastic Dynamic Prediction》以来,概率预报已经深入人心,改变了人们对气象预报的看法。Epstein认为,即使大气的动力机制本身是确定性的,由于观测有限,同时模式也非完美,我们永远无法确切知道所谓的“真值”。所以对大气的预报应该是概率的,而非确定性的。如何将概率引入气象预报呢?相较于过去只做一个预报,我们可以从不同的初始条件出发,或使用不同的模式,同时进行多组预报,每个预报成员都可以看作是系统概率分布的一个随机采样,这就是集合预报。
集合卡尔曼滤波(EnKF)是基于集合预报的同化方法。它可以结合模式和观测的信息,得到更准确的后验初始场。在集合卡尔曼滤波中,对模式不确定性的估计是至关重要的一步,模式不确定性量化表示为一个误差协方差矩阵$\mathrm {P}^b$,由预报集合估计。但在实践中我们会发现,对$\mathrm {P}^b$的估计常常受集合数量的影响。例如,将协方差矩阵化为相关系数矩阵,用较少集合估计出的$\mathrm {P}^b$会在某些位置出现虚假相关,这些虚假相关在使用足够多集合去估计$\mathrm {P}^b$时是不存在的(图1)。
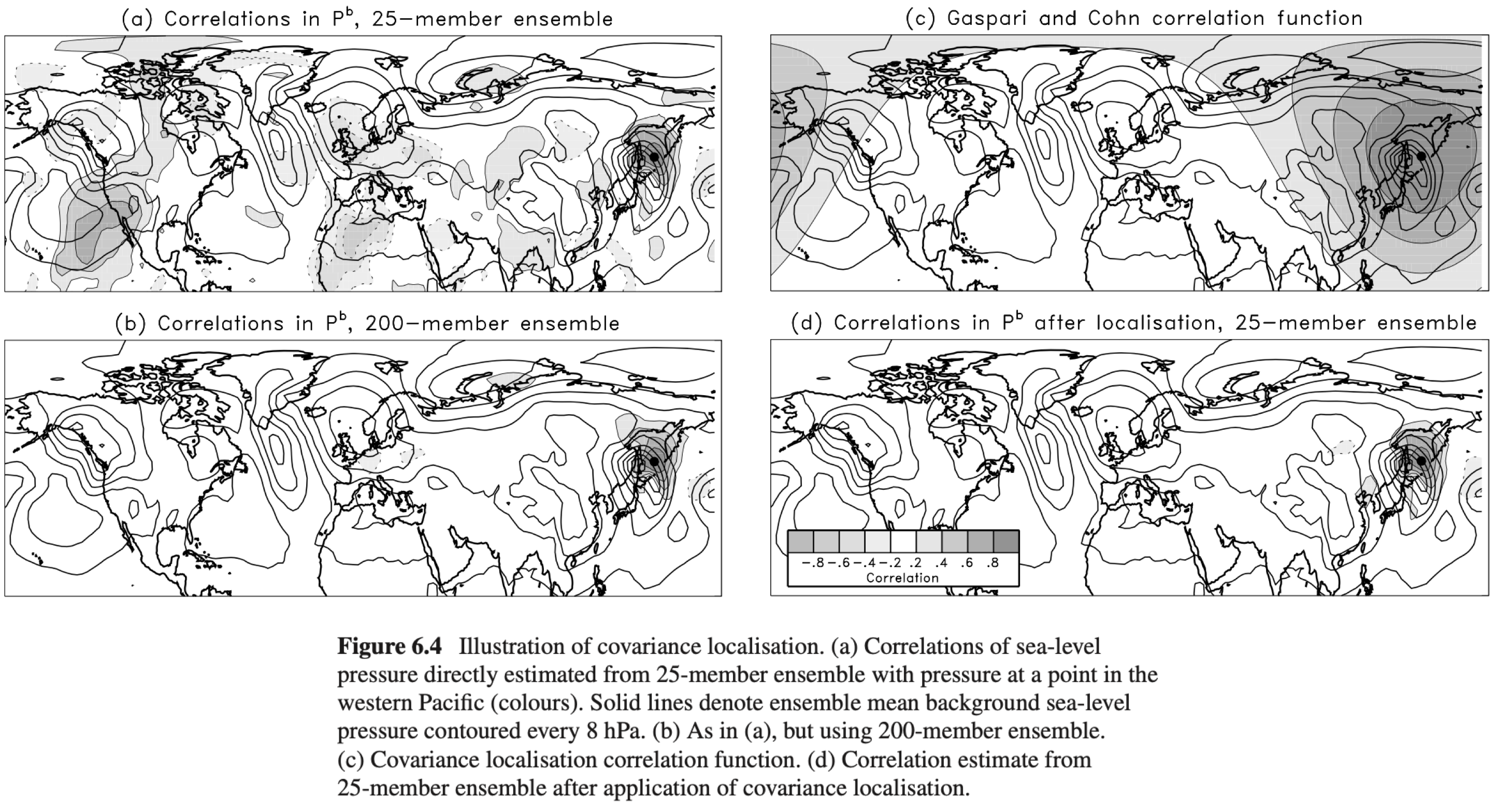
这些虚假相关,其实是由于采样样本数量不足导致的误差,称为采样误差(Sampling Error)。
采样误差
采样误差其实在统计推断中无处不在。当我们想要估计总体(Population)分布的某个参数,通常并不会,或者不能统计到总体的每一个个体,而只会取总体的一部分,作为我们的样本(Sample),从样本来估计总体的参数。比如我们想要知道总体分布的期望大概是多少,就会用样本的均值作为对期望的一个估计。
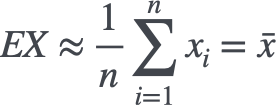
假如我们现在要估计一个服从正态分布$X \sim \mathcal{N}(0.5,\sigma ^2) $总体的均值,总体容量为10亿个(若总体容量可为无穷多,总体的均值就严格等于总体分布的期望)。从总体里随机抽取100个样本,以这100个样本的均值作为对总体均值的估计。算出来这100个样本的均值,几乎一定不会等于0.5,总是偏大或偏小一点。而且,重复多次采样,每次估计到的均值也大概率不会相同。多次采样估计出的均值,也会构成一个分布
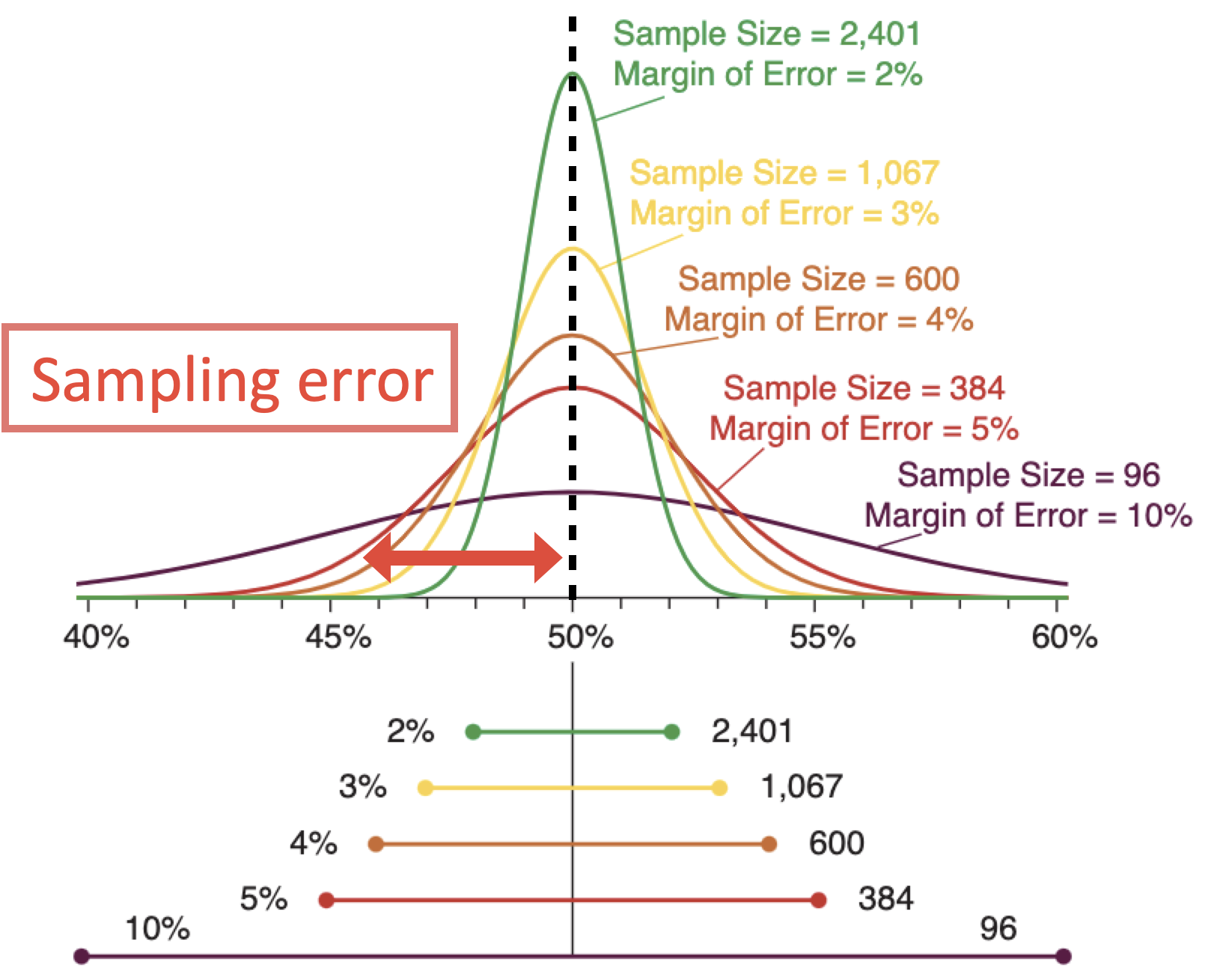
每次估计得到的均值与真实的期望的差距就是采样误差。抽取2000个样本和抽取100个样本去估计均值,其采样误差的范围是不同的。2000个样本估计得到的均值分布高高瘦瘦,100个样本得到的均值分布相比起来就矮胖一些。显然,我们更希望均值像2000个样本估计的那样,更接近真实的期望,同时又有更小的方差。有一个指标来量化采样误差的大小范围,叫误差限(Margin of Error)
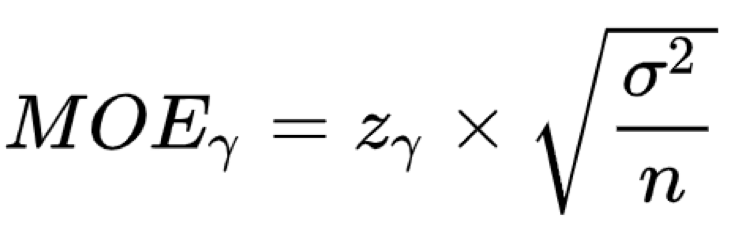
它与总体分布本身的方差有关,同时也与样本数量n有关。容易看出,样本数量越大,误差限就越小,表示采样误差就越小。
下面举一个稍复杂点的例子,这次不再是估计单变量的分布特征,而是估计多变量分布的相关特征。假如有两个变量$X_1,X_2$都服从正态分布$X_1,X_2 \sim \mathcal{N}(0,1) $,它们的协方差为$c_{12}$,可用一个回归方程描述二者的关系

其中
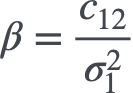
现在要用采样的方式估计回归系数$\beta$,我们看一下使用不同样本数量估计得到的结果
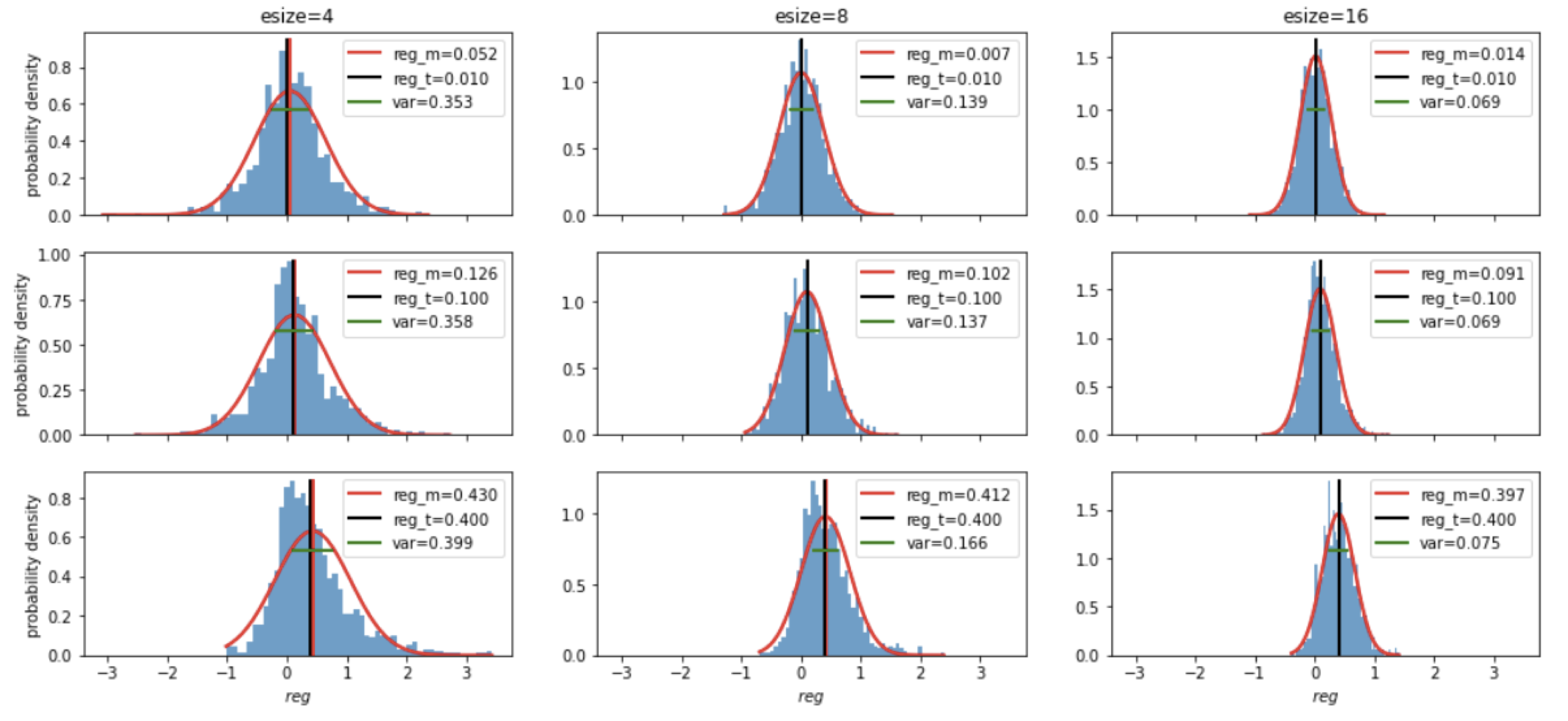
同样的,样本数量越多,估计量分布就越集中,越接近真实值。
换成估计相关系数试试。
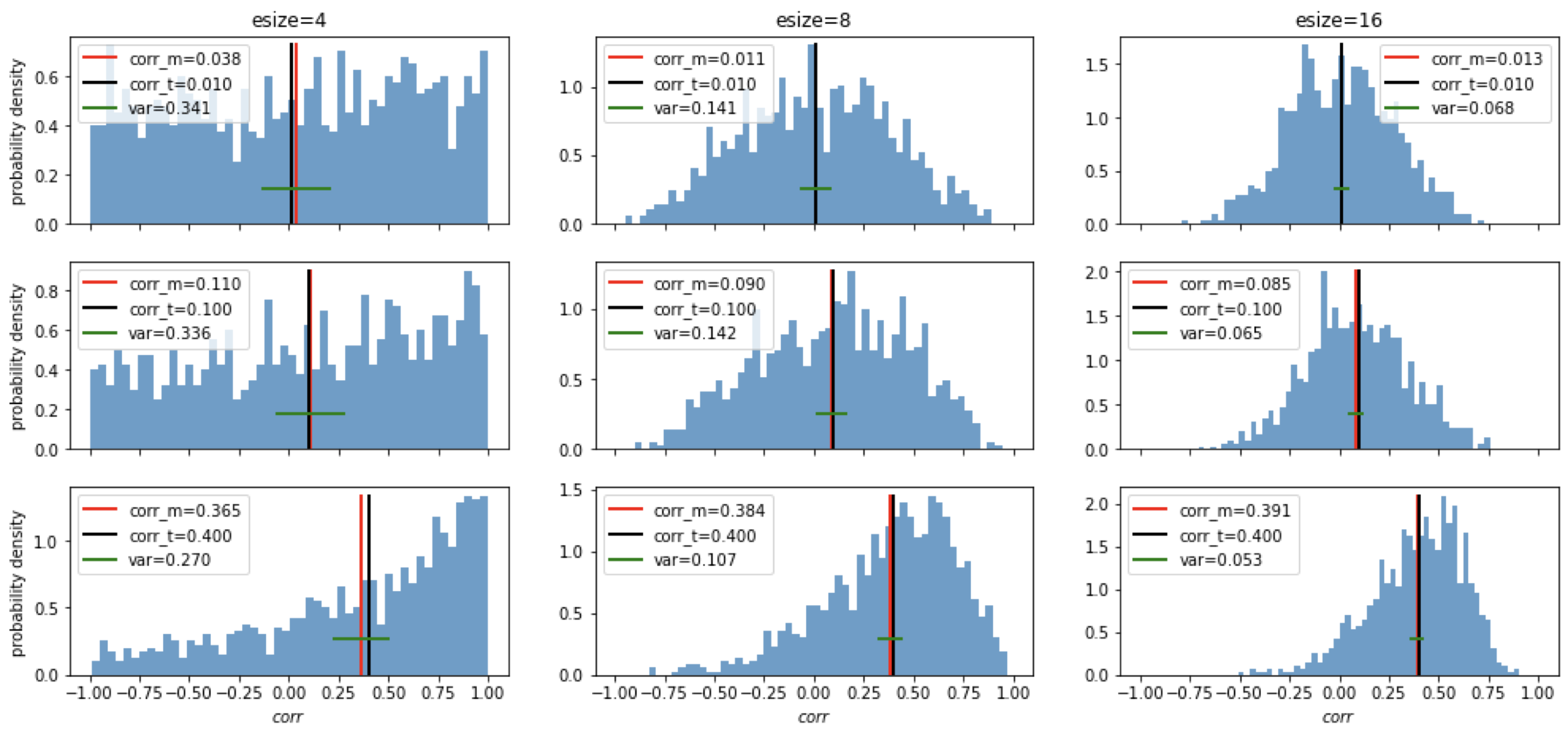
这次稍有不同,相关系数是有边界的量([-1,1]),所以估计量不再满足正态分布,但同样能看出样本数量越多,估计量分布越集中且越靠近真值。所以结论是一致的:样本数量越大,采样误差就越小。
消减虚假相关:局地化方法
既然增大样本数量就能减小采样误差,那何不用更多的预报集合呢。的确,在钱不是问题的情况下,采样误差也不成问题。但现实是,集合预报需要耗费大量的计算资源,无限度地增加集合数量目前尚不可行。那么问题就变成,如何在有限的条件下,更大限度地提取高质量的信息。具体到EnKF,如何用100个集合成员就达到或逼近2000个集合成员估计的准确度呢。
Hamill在2001年的文章中指出,两变量间的相关系数越小,使用的集合数量越少,对协方差估计的相对误差就越大
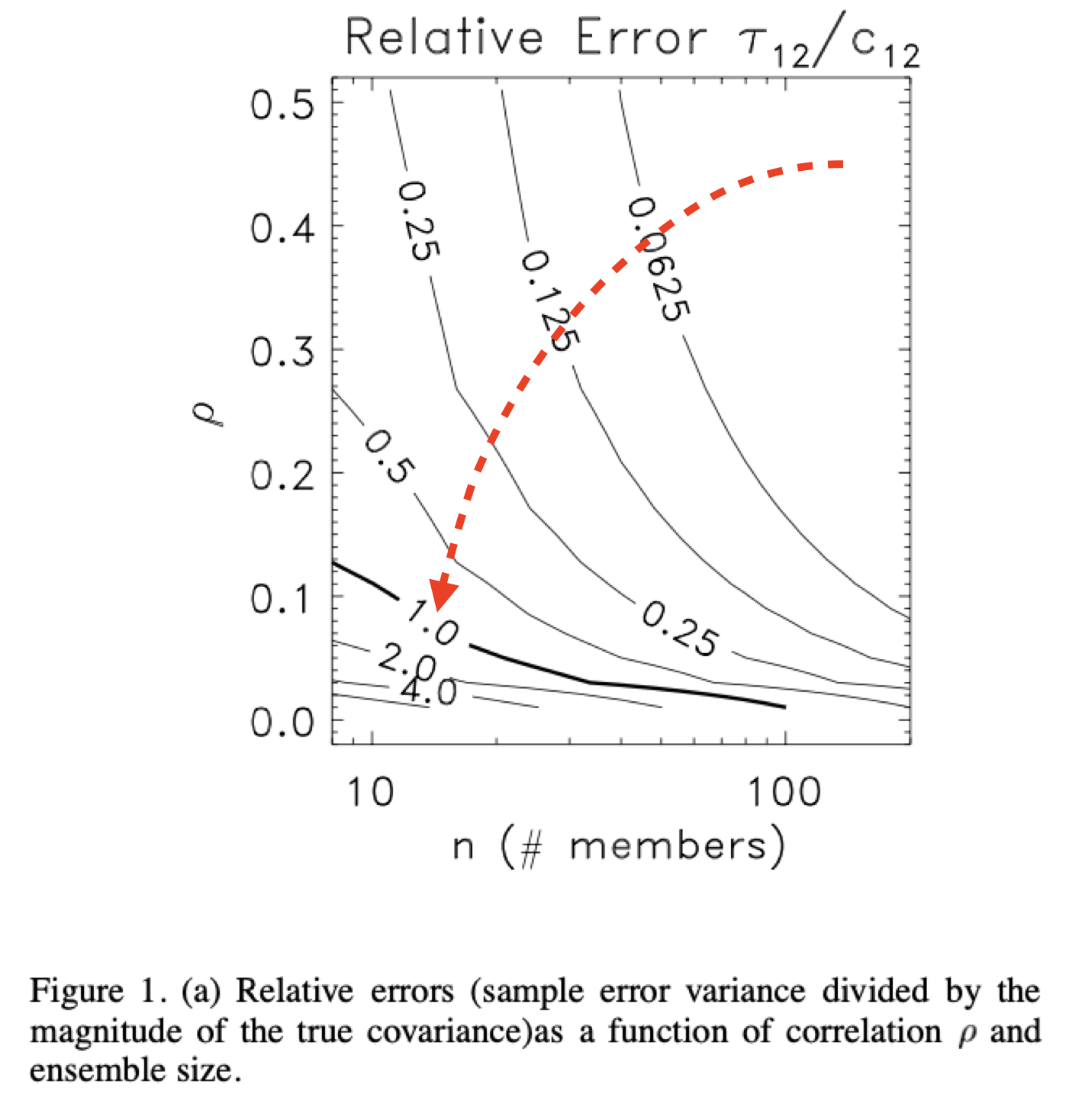
其中协方差$c_{12}$采样误差的方差为
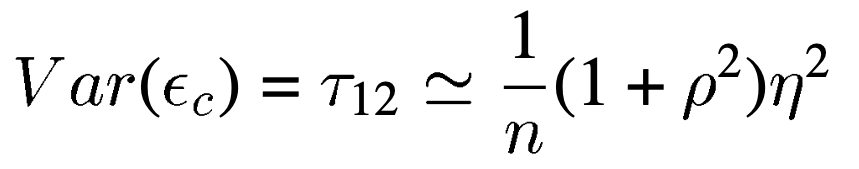
所以在本应接近无相关的位置出现虚假相关,其影响并非是无足轻重的。那么,如何消除虚假相关,用更少的集合得到更准确的估计效果呢。
前面提到,我们的问题是在如何在100个集合的限制条件下,提取更多更好的信息。其实还有另一种思路,如果我们无法提取更多的信息,是否可以人为地加入一些先验信息?比如,我们相信随着距离增大,两变量间的相关应该是减小的,那么能不能定义一个随距离减小的函数,作用在协方差矩阵$\mathrm {P}^b$上呢?事实上的确能这么做,Gaspari and Cohn函数就是这么一个函数。它由一个单一可调参数确定形状,作用在协方差矩阵或卡尔曼增益上以消除虚假相关。这种类似的方法在数据同化中都称为局地化方法。所以,一个好的局地化函数,也是提升集合同化方法表现的一块重要拼图。
参考
Gaspari, G., and S. E. Cohn, 1999: Construction of correlation functions in two and three dimensions. Quart. J. Roy. Meteor. Soc., 125, 723–757.
Hamill, Thomas M., Jeffrey S. Whitaker, and Chris Snyder. “ Distance-Dependent Filtering of Background Error Covariance Estimates in an Ensemble Kalman Filter”. Monthly Weather Review 129.11 (2001): 2776-2790.
Hamill, Thomas. (2004). Ensemble-based atmospheric data assimilation. Predictability of Weather and Climate. 10.1017/CBO9780511617652.007.