“Having heard without comprehension they are like the deaf; this saying bears witness to them: present they are absent.’’ — Heraclitus
二辩聊过,中国学生心算能力普遍比美国学生高很多,因为背乘法表是中国小学生的必修技能。但单论计算效率而言的话,计算器也已经不是什么稀奇的高科技产品了,假如一个熟练掌握乘法表的中国小学生和一个熟练使用计算器的美国小学生比赛算术,恐怕是美国小学生胜出,而且题目越难算越是如此。那么背乘法表的意义何在?
一部记录高中教育改革的记录片(《真实生长》),北京十一中的一名历史教师和教理科的教师辩论,该不该让学生熟背历史事件的时间节点。历史老师认为这应是学生基本素养的一部分。理科老师认为学生只需花几分钟查表就能知道的东西,无需死记硬背。
费曼去上生物学系的课,老师要他读一篇论文然后做报告。论文需要他了解猫全身肌肉的分布,于是他花十来分钟去图书馆查到了“猫地图”。当他作报告画“猫地图”的时候,生物系的学生说,“这些我们都知道”。费曼说“哦,你们知道,怪不得我能这么快就赶上你们这些学了四年生物的。”15分钟能找的到的东西,他们却把时间都浪费在死记硬背这些东西上。
在巴西的一家饭馆,费曼和一个日本人比赛算术。日本人精通算盘。开始是简单的加法,然后是乘法,除法,费曼都比不过日本人。最后一题求1729.03的立方根,费曼用微积分的近似法很快得到结果约是12.003,打败了日本人。费曼认为,这是因为他真的“懂数字”。
第四个例子似乎和第一个例子有矛盾。在较量计算速度的这个比赛里,似乎掌握更先进的工具就具有优势。日本人用算盘,算盘已经是比乘法表心算更强大的工具了,但最后为什么还是败给了看似简单的微分近似法则?乘法表,计算器,算盘,近似法则其实都是一些规则,或者工具,工具是被用来解决问题,从而有了低效和高效之分。但这些辩论到底是围绕什么?
费曼还举过一个例子。他的爸爸指着树上的一只鸟问他:“你知道这是什么鸟吗?这是brown-throated thrush,它在葡萄牙语里叫Bom da Peida,意大利语里,它叫Chutto Lapittida,中文读作Chung-long-tah,日语叫作Katano Teketa,不一而足。你可以用你想了解的所有语种,去称呼这只鸟,但当你叫出它的名字之后,你其实对这只鸟还是一无所知。现在,让我们来好好看看这只鸟,观察它在做什么。”
2022年3月17日更新
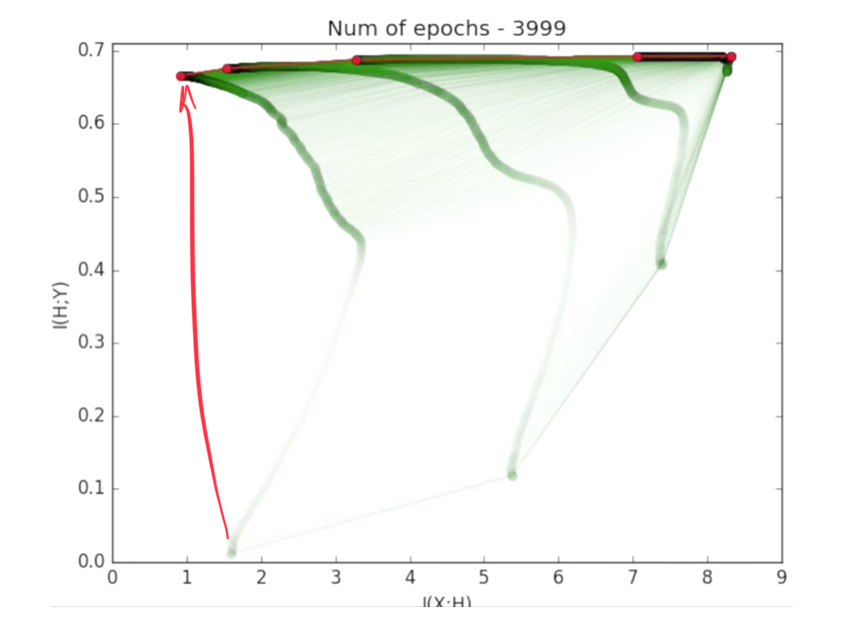
今天看到一个2017年的talk,Naftali Tishby教授讲机器学习中的信息论Information Theory of Deep Learning,很mind-blowing(看得我小脸通红)。
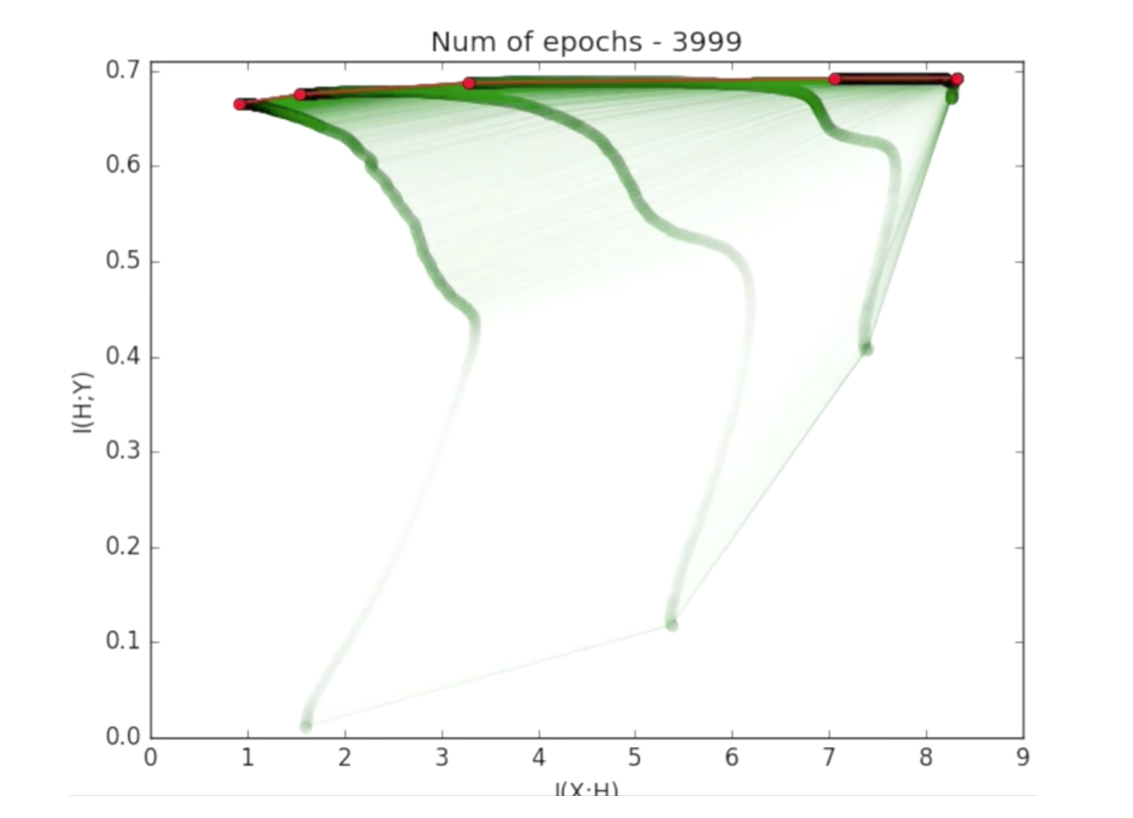
这张图是Tishby talk的精髓,用一句话概括就是“先读厚,再读薄。”
想起来几年前问过我很喜欢的日本dancer Yu-mah一个问题,想要跳得很棒的话,那些日复一日对基本功的重复训练,是不是一个必经的阶段?现在想想,当年naïve的我真的问了一个哲学问题。我大概是想知道存不存在这样一条路线